Lösungen zu Aviatik 2008/2

Version vom 4. Januar 2010, 10:19 Uhr von Admin (Diskussion | Beiträge) (→‎Aufgabe 5)
(Unterschied) ← Nächstältere Version | Aktuelle Version (Unterschied) | Nächstjüngere Version → (Unterschied)

Aufgabe 1

  1. Das Niveau in den beiden Tanks liegt am Schluss des Ausgleichs auf einer Höhe von [math]h=\frac{A_1h_1+A_2h_2}{A_1+A_2}[/math] =14 m. Dabei ist eine Masse von [math]\Delta m=\varrho A_1 (h_1-h)[/math] = 1200 t im Mittel um vier Meter hinunter geflossen, womit eine Energie von [math]W_{diss}=\Delta m g\Delta \overline h[/math] = 47 MJ dissipiert worden ist.
  2. Wenn in zwei Stunden 1500 m3 Kerosin durch die Leitung fliessen, ist der mittlere Volumenstrom 0.208 m3/s stark. Zu beginn betrug der Volumenstrom das Doppelte und nach einer halben Stunde das Anderthalbfache des zeitlichen Mittels, was eine Stärke von 0.313 m3/s ergibt.
  3. In der ersten halben Stunde betrug der mittlere Volumenstrom 0.365 m3/s. Folglich sind in der ersten halben Stunde 656 m3 durch die Leitung geflossen. Dieser Teilausgleich hat das Niveau im ersten Tank um 0.875 m auf 15.125 m gesenkt und im zweiten Tank um 2.625 m auf 10.625 m angehoben.
  4. Die Prozessleistung ist gleich Massenstromstärke mal Unterschied im Gravitationspotenzial oder gleich [math]P=\varrho g \Delta h I_V[/math] = 11kW.

Aufgabe 2

  1. Die maximale Stromstärke beträgt 1.54 A. Zu diesem Zeitpunkt wird im Widerstand der Spule die grösste Leistung dissipiert [math]P=RI^2[/math] = 2.37 W.
  2. Der Widerstand der Spule ist so klein, dass er den Schwingkreis nur schwach stört. Folglich darf behauptet werden, dass der Kondensator dann entladen ist, wenn der Strom am stärksten ist. Nun lässt sich aus dem Stromstärke-Zeit-Diagramm entnehmen, wie viel Ladung aus dem Kondensator weg fliesst (Fläche unter der Kurve bis zum Zeitpunkt 0.00024 s). Die Kapazität ist dann gleich der weg geflossenen Ladung dividiert durch die anfänglich angelegte Spannung von 50 V, also [math]C=\frac{Q}{U}[/math] = 5μF.
  3. Zum Zeitpunkt Null liegt über der Spule eine Spannung von 50 V. Weil noch kein Strom fliesst, dient die ganze Spannung der Änderung der Stromstärke. Diese Änderungsrate ist im Stromstärke-Zeit-Diagramm als Steigung der Kurve im Zeitnullpunkt zu entnehmen [math]L=\frac{U}{\dot I}[/math] = 5 mH.
  4. Die magnetisch gespeicherte Energie wächst quadratisch mit der Stromstärke [math]W=\frac{L}{2}I^2[/math]. Somit gilt [math]\frac{W_2}{W_1}=\frac{I_2^2}{I_1^2}[/math] = 0.84. Pro Periode nimmt die Energie um 16% ab (die Stromstärke aber nur um etwa 8 %).

Aufgabe 3

Schaltkreis zu 1

Im ersten Moment ist sind die Ladung auf der Kapazität und der Strom durch die Induktivität gleich Null. Die Kapazität verhält sich dann wie ein Kurzschluss (der Strom fliesst ohne Spannung) und die Induktivität wie ein offener Schalter (der Strom muss zuerst anwachsen). Nach längerer Zeit ist der Kondensator voll geladen. Dann fliesst trotz angelegter Spannung kein Strom mehr. Umgekehrt hat der Strom durch die Induktivität die volle Stärke erreicht. Es braucht dann keine Spannung mehr, um den Strom in seiner Stärke zu ändern.

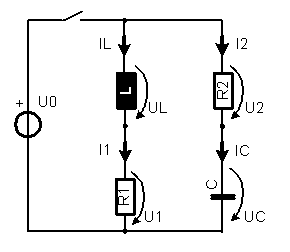
1. Im ersten Moment fliesst durch den linken Kreis keinen Strom und die Spannung liegt über der Induktivität. Im rechten Kreis begrenzt nur der Widerstand 2 den Strom. Nach längerer Zeit wird im linken Kreis der Strom nur durch den Widerstand 1 begrenzt. Dann liegt im rechten Kreis die Spannung über der Kapazität, ohne dass ein Strom fliesst.

t UL IL U1 I1 U2 I2 UC IC
s V A V A V A V A
0 5 0 0 0 5 0.5 0 0.5
∞ 0 1 5 1 0 0 5 0


Schaltkreis zu 2

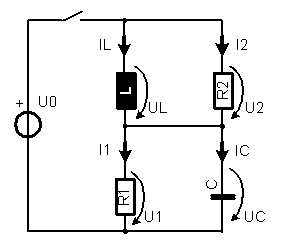
2. Die mittlere Verbindung ändert zu den fraglichen Zeitpunkten nichts am Verhalten des Systems. Im ersten Moment ist die Spannung über der Kapazität gleich Null, weil der Kondensator überhaupt noch nicht geladen ist. Folglich muss die Spannung über dem parallel dazu geschalteten Widerstands 2 auch gleich Null sein. Nach längerer Zeit ist die Spannung über der Induktivität gleich Null, weil der Strom nicht mehr wächst. Die Spannung über dem parallel dazu geschalteten Widerstand 2 ist deshalb auch gleich Null.

t UL IL U1 I1 U2 I2 UC IC
s V A V A V A V A
0 5 0 0 0 5 0.5 0 0.5
∞ 0 1 5 1 0 0 5 0

Aufgabe 4

Die Relativgeschwindigkeit des Vogels geht linear mit der Zeit zurück, d.h. die Beschleunigung ist konstant.

  1. Die zur Verfügung stehende Zeit ist gleich der Verformung der Knautschzone dividiert durch die mittlere Geschwindigkeit oder gleich der doppelten Verformung durch die Anfangsgeschwindigkeit [math]\Delta t=\frac{\Delta s}{\overline v}=\frac{2\Delta s}{v_0}[/math] = 2.667 ms.
  2. Eine Kraft ist eine Impulsstromstärke bezüglich eines Systems [math]F=\frac{\Delta p}{\Delta t}=\frac{mv_0^2}{2\Delta s}[/math] = 90 kN (die Kraft auf das Flugzeug beträgt mehr als das Fünftausendfache des Vogelgewichts!).
  3. Zum Zeitpunkt Null fällt der Impulsstrom in der Knautschzone über die volle Geschwindigkeit von 150 m/s. Somit ist die vom Impulsstrom in der Verformungszone frei gesetzte Prozessleistung gleich [math]P=v_0F[/math] = 13.5 MW.
  4. Die vom Impulsstrom in der Knautschzone frei gesetzte Energie ist gleich (konstante) Kraft mal Verformung [math]W=\Delta s F=\frac m2 v_0^2[/math] = 18 kJ. Die vom Impulsstrom frei gesetzte Energie entspricht damit gerade der kinetischen Energie des Vogels relativ zum Flugzeug.

Aufgabe 5

Gemäss dem Schnittprinzip wirken auf das Bierfass in vertikaler Richtung nur zwei Kräfte ein: die direkt nachweisbare Oberflächenkraft, oft Normalkraft genannt, und die nicht direkt nachweisbare, am ganzen Volumen angreifende Gewichtskraft. Die Waage misst den durchfliessenden Impulsstrom, welcher der Normalkraft entspricht.

  1. Vom erdfesten Bezugssystem aus betrachtet (Sicht von Claudia) wirkt eine nach oben gerichtete Normalkraft von 98.1 N und eine nach unten wirkende Gewichtskraft von 147.2 N auf das Bierfass ein. Die resultierende Kraft, welche für die Beschleunigung verantwortlich ist, beträgt 49.1 N und wirkt nach unten.
  2. Klaus sieht im Prinzip die gleichen Kräfte. Nur müssen diese das Fass im Gleichgewicht halten. Deshalb hat die Gewichtskraft für ihn (Bezugssystem Gondel) eine Stärke von 98.1 N.
  3. Das Fass und die Gondel sind nur aus der Sicht von Claudia beschleunigt. Die Beschleunigung des Fasses und damit der Gondel sind gleich resultierende Kraft durch die Masse des Fasses, also [math]a=\frac{F_{Res}}{m}[/math] = 3.27 m/s2. Daraus berechnet sich die Geschwindigkeit auf der Kreisbahn [math]v=\sqrt{ar}[/math] = 2.56 m/s.
  4. Am tiefsten Punkt zeigt die resultierende Kraft nach oben und hat einen Wert von 98.1 N. Folglich ist die Beschleunigung gleich 6.54 m/s2.

Bemerkungen:

  1. Der Begriff Zentripetalkraft, der oft für die resultierende Kraft bei einer Kreisbewegung verwendet wird, ist überflüssig und auch irreführend. Überflüssig, weil man aufgrund des Schnittprinzips schon alle Kräfte gefunden hat. Irreführend, weil man nicht mehr Namen vergeben sollte, als unabhängige Kräfte vorhanden sind.
  2. Der Begriff Zentrifugalkraft ist hier völlig fehl am Platz. Die Zentrifugalkraft tritt nur auf, wenn sich der Beobachter im rotierenden Bezugssystem befindet. Klaus steht aber in der Gondel und die rotiert nicht, sonder bewegt sich nur im Kreis herum.
  3. Eine Beschleunigung kann man nicht spüren. Was man spürt, sind die Auswirkungen des lokal nachweisbaren Gravitationsfeldes. Klaus kann die Stärke dieses Feld erklären, indem er die normale Feldstärke an der Erdoberfläche nimmt und mit einem homogenen Trägheitsfeld überlagert. Die Stärke des homogenen Feldes ist gleich minus die Beschleunigung der Gondel gegen die Erde.

Aufgabe 6

Dieses Modell ist unter Fahrwerk-Fallversuch besprochen.

Aufgabe

Abgerufen von „http://systemdesign.ch/index.php?title=Lösungen_zu_Aviatik_2008/2&oldid=9481“