Katze: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
==Flüssigkeitsbild== |
==Flüssigkeitsbild== |
||
Das einfachste Modell der Katze besteht aus zwei Drehimpulsspeichern, die ihr Massenträgheitsmoment stark verändern können. Diese Veränderung erzeugt die Katze nicht nur durch Ausstrecken und Einziehen der beiden Beinpaare. Wie schon die Filmaufnahmen von Marey gezeigt haben, kann die Katze die Masse in der vorderen und der hinteren Hälfte stark axial ausrichten oder radial verteilen. |
Das einfachste [[Modell]] der Katze besteht aus zwei Drehimpulsspeichern, die ihr Massenträgheitsmoment stark verändern können. Diese Veränderung erzeugt die Katze nicht nur durch Ausstrecken und Einziehen der beiden Beinpaare. Wie schon die Filmaufnahmen von Marey gezeigt haben, kann die Katze die Masse in der vorderen und der hinteren Hälfte stark axial ausrichten oder radial verteilen. |
||
Die eigentliche Drehung kann nun in vier Intervalle unterteilt und im Flüssigkeitsbild dargestellt werden. In den ersten beiden Zeitabschnitten ist das Trägheitsmoment des vorderen Teils klein und das des hinteren Teils groß. Danach wird die Masse vorne nach außen verlagert und hinten möglichst Nahe zur Körperachse gebracht. Im ersten Intervall pumpt die Katze Drehimpuls von hinten nach vorne, indem sie die entsprechenden Muskeln spannt. Im zweiten Intervall lässt sie den Drehimpuls wieder zurück fließen. Danach kommt die Katze völlig verdreht zur Ruhe und verändert schlagartig die Massenverteilung. In den beiden letzten Intervallen pumpt sie zuerst Drehimpuls in den hintern Teil und lässt ihn dann wieder zurückfließen. Dabei bewegt sich der vordere Teil etwas zurück und der hintere Teil macht seine entscheidende Drehung. |
Die eigentliche Drehung kann nun in vier Intervalle unterteilt und im [[Flüssigkeitsbild]] dargestellt werden. In den ersten beiden Zeitabschnitten ist das Trägheitsmoment des vorderen Teils klein und das des hinteren Teils groß. Danach wird die Masse vorne nach außen verlagert und hinten möglichst Nahe zur Körperachse gebracht. Im ersten Intervall pumpt die Katze [[Drehimpuls]] von hinten nach vorne, indem sie die entsprechenden Muskeln spannt. Im zweiten Intervall lässt sie den Drehimpuls wieder zurück fließen. Danach kommt die Katze völlig verdreht zur Ruhe und verändert schlagartig die Massenverteilung. In den beiden letzten Intervallen pumpt sie zuerst Drehimpuls in den hintern Teil und lässt ihn dann wieder zurückfließen. Dabei bewegt sich der vordere Teil etwas zurück und der hintere Teil macht seine entscheidende Drehung. |
||
==SD-Modell== |
==SD-Modell== |
||
[[Bild:KatzeSD.jpg|thumb|SD-Modell der Katze]] |
|||
Das Grobmodell lässt sich verbessern, indem „Drehimpuls pumpen“ und „Massenträgheitsmoment ändern“ parallel ablaufen. Beschreiben wir also den Drehimpulsstrom mit einer Cosinusfunktion und die beiden Massenträgheitsmomente mit je einer Konstante (''J<sub>0</sub>'') plus überlagerter Cosinusfunktion. Damit die gewünschte Drehung eintritt, muss die Frequenz beim Massenträgheitsmoment halb so groß wie beim Drehmoment sein. |
|||
''Relationen und Parameter:'' |
|||
{|border ="1" |
|||
!BerkeleyMadonna-Code |
|||
!Bemerkung |
|||
|- |
|||
|MKatze = Mmax*cos(2*pi/Periode*time) |
|||
|Drehimpulsstrom |
|||
|- |
|||
|IW_h = w_h*MKatze |
|||
|Leistung hinten |
|||
|- |
|||
|IW_v = w_v*MKatze |
|||
|Leistung vorne |
|||
|- |
|||
|w_h = L_h/J_h |
|||
|Winkelgeschwindigkeit hinten |
|||
|- |
|||
|w_v = L_v/J_v |
|||
|Winkelgeschwindigkeit vorne |
|||
|- |
|||
|J_h = J0+cos(pi/Periode*time)*Delta_J |
|||
|Massenträgheit hinten |
|||
|- |
|||
|J_v = J0-cos(pi/Periode*time)*Delta_J |
|||
|Massenträgheit vorne |
|||
|- |
|||
|Wrot_h = 0.5*J_h*w_h^2 |
|||
|Rotationsenergie hinten |
|||
|- |
|||
|Wrot_v = 0.5*J_v*w_v^2 |
|||
|Rotationsenergie vorn |
|||
|- |
|||
|Mmax = 1.816 |
|||
|Amplitude des Drehimpulsstromes |
|||
|- |
|||
|J0 = 0.01 |
|||
|mittlere Massenträgheit |
|||
|- |
|||
|Delta_J = 0.007 |
|||
|Änderung der Massenträgheit |
|||
|- |
|||
|Periode = 0.5 |
|||
|zur Änderung von ''J'' |
|||
|} |
|||
==Simulation== |
==Simulation== |
||
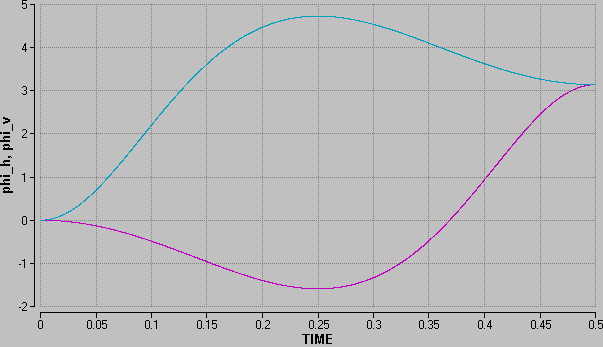
Das folgende Diagramm zeigt das Drehwinkel-Zeit-Verhalten der beiden Katzenhälften. Nach 0.25 Sekunden ist die Katze um den Winkel 2π (360°) verdreht. |
|||
[[Bild:KatzeSim1.png]] |
|||
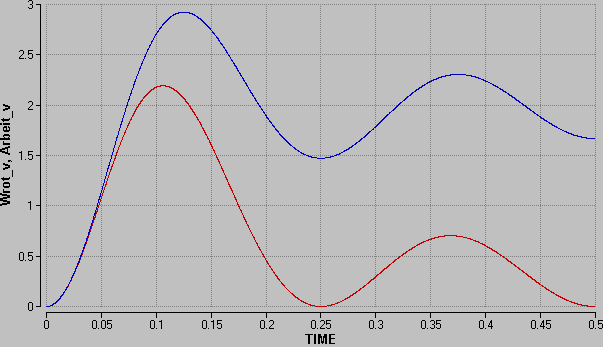
Das zweite Diagramm zeigt den zeitlichen Verlauf der Arbei des Drehmomentes (Zeitintegral über den [[zugeordneter Energiestrom|zugeordneten Energiestrom]]) auf die vordere Katzenhälfte und parallel dazu die Rotationsenergie dieses Teils der Katze. |
|||
[[Bild:KatzeSim2.png]] |
|||
Die [[Rotationsenergie]], die Energie, die zu jedem Zeitpunkt durch den Drehimpulsausgleich mit der Erde bei konstant gehaltenem Massenträgheitsmoment freigesetz werden könnte, entspricht nicht der Arbeit des Drehmomentes auf den vorderen Teil der Katze. Die Rotationsenergie ist eine reine Bilanzgrösse. Wann wo welche [[Energie]] umgesetzt wird, hängt mit der konkreten Prozessführung zusammen. |
|||
==Links== |
|||
*[http://www.youtube.com/watch?v=hZit4v4ERpM Katze] auf Youtube |
|||
[[Kategorie: Modelle]] [[Kategorie: RotMod]] |
[[Kategorie:Rot]] [[Kategorie: Modelle]] [[Kategorie: RotMod]] |
||
Aktuelle Version vom 7. März 2011, 06:02 Uhr
Warum fallen Katzen immer auf die Füsse?
Im Jahr 1894 erging von der Pariser Akademie der Wissenschaften ein Aufruf, »eine physikalische Erklärung zu geben, wie es eine Katze fertig bringe, beim Fallen aus größerer Höhe stets mit den Füßen voran auf den Boden zu kommen«. Das Rätsel löste schließlich der Arzt Étienne Jules Marey. Marey war ein besessener Bastler, der alle möglichen mechanischen Geräte erfand. Unter anderem eine Filmkamera, die den Fall mit sechzig Bildern pro Sekunde festhielt. Bei der Vorführung des Filmes zweifelten einige Physiker immer noch daran, dass die Drehung möglich sei, ohne dass die Katze sich irgendwo abstieß, doch einer erkannte den Trick der Katze. “Welchen Trick, den sogar Physiker kaum durchschauen, wenden Katzen an?
Flüssigkeitsbild
Das einfachste Modell der Katze besteht aus zwei Drehimpulsspeichern, die ihr Massenträgheitsmoment stark verändern können. Diese Veränderung erzeugt die Katze nicht nur durch Ausstrecken und Einziehen der beiden Beinpaare. Wie schon die Filmaufnahmen von Marey gezeigt haben, kann die Katze die Masse in der vorderen und der hinteren Hälfte stark axial ausrichten oder radial verteilen.
Die eigentliche Drehung kann nun in vier Intervalle unterteilt und im Flüssigkeitsbild dargestellt werden. In den ersten beiden Zeitabschnitten ist das Trägheitsmoment des vorderen Teils klein und das des hinteren Teils groß. Danach wird die Masse vorne nach außen verlagert und hinten möglichst Nahe zur Körperachse gebracht. Im ersten Intervall pumpt die Katze Drehimpuls von hinten nach vorne, indem sie die entsprechenden Muskeln spannt. Im zweiten Intervall lässt sie den Drehimpuls wieder zurück fließen. Danach kommt die Katze völlig verdreht zur Ruhe und verändert schlagartig die Massenverteilung. In den beiden letzten Intervallen pumpt sie zuerst Drehimpuls in den hintern Teil und lässt ihn dann wieder zurückfließen. Dabei bewegt sich der vordere Teil etwas zurück und der hintere Teil macht seine entscheidende Drehung.
SD-Modell
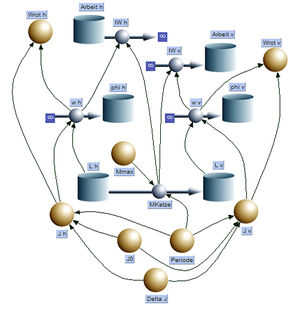
Das Grobmodell lässt sich verbessern, indem „Drehimpuls pumpen“ und „Massenträgheitsmoment ändern“ parallel ablaufen. Beschreiben wir also den Drehimpulsstrom mit einer Cosinusfunktion und die beiden Massenträgheitsmomente mit je einer Konstante (J0) plus überlagerter Cosinusfunktion. Damit die gewünschte Drehung eintritt, muss die Frequenz beim Massenträgheitsmoment halb so groß wie beim Drehmoment sein.
Relationen und Parameter:
| BerkeleyMadonna-Code | Bemerkung |
|---|---|
| MKatze = Mmax*cos(2*pi/Periode*time) | Drehimpulsstrom |
| IW_h = w_h*MKatze | Leistung hinten |
| IW_v = w_v*MKatze | Leistung vorne |
| w_h = L_h/J_h | Winkelgeschwindigkeit hinten |
| w_v = L_v/J_v | Winkelgeschwindigkeit vorne |
| J_h = J0+cos(pi/Periode*time)*Delta_J | Massenträgheit hinten |
| J_v = J0-cos(pi/Periode*time)*Delta_J | Massenträgheit vorne |
| Wrot_h = 0.5*J_h*w_h^2 | Rotationsenergie hinten |
| Wrot_v = 0.5*J_v*w_v^2 | Rotationsenergie vorn |
| Mmax = 1.816 | Amplitude des Drehimpulsstromes |
| J0 = 0.01 | mittlere Massenträgheit |
| Delta_J = 0.007 | Änderung der Massenträgheit |
| Periode = 0.5 | zur Änderung von J |
Simulation
Das folgende Diagramm zeigt das Drehwinkel-Zeit-Verhalten der beiden Katzenhälften. Nach 0.25 Sekunden ist die Katze um den Winkel 2π (360°) verdreht.
Das zweite Diagramm zeigt den zeitlichen Verlauf der Arbei des Drehmomentes (Zeitintegral über den zugeordneten Energiestrom) auf die vordere Katzenhälfte und parallel dazu die Rotationsenergie dieses Teils der Katze.
Die Rotationsenergie, die Energie, die zu jedem Zeitpunkt durch den Drehimpulsausgleich mit der Erde bei konstant gehaltenem Massenträgheitsmoment freigesetz werden könnte, entspricht nicht der Arbeit des Drehmomentes auf den vorderen Teil der Katze. Die Rotationsenergie ist eine reine Bilanzgrösse. Wann wo welche Energie umgesetzt wird, hängt mit der konkreten Prozessführung zusammen.
Links
- Katze auf Youtube