Lösung zu Kreisprozess mit Helium: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 12. April 2011, 13:33 Uhr

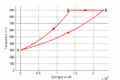
T-S-Diagramm
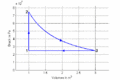
p-V-Diagramm

Im T-S-Diagramme verläuft die isochore Zustandsänderung exponentiell nach oben, die isotherme horizontal und die isobare wiederum exponentiell und weniger steil zurück zum Ausgangspunkt. Im p-V-Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf einer Hyperbel ([math]pV=p_0V_0[/math]) nach rechts unten und zum Schluss auf einer Horizontalen nach links. Im T-S-Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. Im p-V-Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit.
Das universelle Gasgesetz liefert für den unteren Druck einen Wert von p₁ = n * R * T₁ / V₁ = 10 kmol * 8.31 J/K/mol * 300 K / 1 m³ = 249 bar. Der Druck nach dem Aufheizen (1. Teilprozess) beträgt p₂ = n * R * T₂ / V₂ = 10 kmol * 8.31 J/K/mol * 900 K / 1 m³ = 748 bar. Das Volumen beträgt nach dem zweiten, isothermen Teilprozess V₃ = p₂ / p₃ * V₂ = 748 bar / 249 bar * 1 m³ = 3 m³.
Im ersten Teilprozess nimmt die Entropie um [math]\Delta S_{12}=n\hat c_V\ln{\frac{T_2}{T_1}}=\frac 3 2 nR\ln{\frac{T_2}{T_1}}[/math] = 1.5 * 10 kmol * 8.31 J/K/mol * ln(900 K / 300 K) = 137 kJ/K zu. Im dritten, isobaren Teilprozess nimmt die Entropie um 5/3 dieses Wertes, also um 228 kJ/K ab, weil die Wärmekapazität bei konstantem Druck 5/3 der Wärmekapazität bei konstantem Volumen ist. Die Differenz von 91 kJ/K muss im zweiten, isothermen Teilprozess aus einem Wärmebad zugeführt werden.
Die total erzeugte Entropie ist die Differenz zwischen der Entropie, die im letzten Teilschritt der Umgebung zugeführt wird, und jener, die der Ofen in den beiden ersten Teilschritten abgibt. Im ersten, isochoren Teilprozess wird dem Helium die thermische Energie [math]W_{therm12} = n \hat c_V \Delta T[/math] = 10 kmol * 1.5 * 8.31 J/K/mol * 600 K = 74.8 MJ zugeführt. Bei der nachfolgenden isothermen Zustandsänderung nimmt das Gas zusätzlich die thermische Energie [math]W_{therm23} = T_2 \Delta S_{23} = T_2 n R \ln{\frac{V_3}{V_2}}[/math] = 900 K * 10 kmol * 8.31 J/K/mol * ln(3 m3 / 1 m3) = 82.2 MJ auf. Um die Energie für diese beiden Teilprozesse aus dem Ofen abzutransportieren, muss der Ofen die folgende Entropiemenge bei seiner konstanten Temperatur von 1000 K abgeben: [math]S_{Ofen}=\frac{W_{therm12} + W_{therm23}}{T_{Ofen}}=\frac{74.8 MJ + 82.2 MJ}{1000 K}[/math] = 157 kJ/K. Im dritten, isobaren Teilprozess gibt das Helium die thermische Energie [math]W_{therm31} = n \hat c_p \Delta T = n \frac 5 2 R \Delta T[/math] = 10 kmol * 2.5 * 8.31 J/K/mol * 600 K = 125 MJ ab. Diese Energie muss bei einer Temperatur von 280 K von der Entropie [math]S_{Um}=\frac{W_{therm31}}{T_{Um}}[/math] = 125 MJ / 280 K = 446 kJ/K in die Umwelt hinein getragen werden. Wie oben geschrieben, wird die Differenz zwischen der von der Umwelt aufgenommenen und der vom Ofen abgegebenen Entropie erzeugt. Diese Differenz beträgt 446 kJ/K - 157 kJ/K = 289 kJ/K.

Aufgabe

@@ Zeile 6: / Zeile 6: @@
 #Das [[ideales Gas|universelle Gasgesetz]] liefert für den unteren Druck einen Wert von p<sub>1</sub> = n * R * T<sub>1</sub> / V<sub>1</sub> = 10 kmol * 8.31 J/K/mol * 300 K / 1 m<sup>3</sup> = 249 bar. Der Druck nach dem Aufheizen (1. Teilprozess) beträgt p<sub>2</sub> = n * R * T<sub>2</sub> / V<sub>2</sub> = 10 kmol * 8.31 J/K/mol * 900 K / 1 m<sup>3</sup> = 748 bar. Das Volumen beträgt nach dem zweiten, isothermen Teilprozess V<sub>3</sub> = p<sub>2</sub> / p<sub>3</sub> * V<sub>2</sub> = 748 bar / 249 bar * 1 m<sup>3</sup> = 3 m<sup>3</sup>.
 #Im ersten Teilprozess nimmt die Entropie um <math>\Delta S_{12}=n\hat c_V\ln{\frac{T_2}{T_1}}=\frac 3 2 nR\ln{\frac{T_2}{T_1}}</math> = 1.5 * 10 kmol * 8.31 J/K/mol * ln(900 K / 300 K) = 137 kJ/K zu. Im dritten, isobaren Teilprozess nimmt die Entropie um 5/3 dieses Wertes, also um 228 kJ/K ab, weil die Wärmekapazität bei konstantem Druck 5/3 der Wärmekapazität bei konstantem Volumen ist. Die Differenz von 91 kJ/K muss im zweiten, isothermen Teilprozess aus einem Wärmebad zugeführt werden.
-#Im ersten, isochoren Teilprozess wird dem Helium die thermische Energie <math>W_{therm12} = n \hat c_V \Delta T</math> = 10 kmol * 1.5 * 8.31 J/K/mol * 600 K = 74.8 MJ zugeführt. Bei der nachfolgenden isothermen Zustandsänderung nimmt das Gas zusätzlich die thermische Energie <math>W_{therm23} = T_2 \Delta S_{23} = T_2 n R \ln{\frac{V_3}{V_2}}</math> = 900 K * 10 kmol * 8.31 J/K/mol * ln(3 m3 / 1 m3) = 82.2 MJ auf. Um die Energie für diese beiden Teilprozesse aus dem Ofen abzutransportieren, muss der Ofen die folgende Entropiemenge bei seiner konstanten Temperatur von 1000 K abgeben: <math>S_{Ofen}=\frac{W_{therm12} + W_{therm23}}{T_{Ofen}}=\frac{74.8 MJ + 82.2 MJ}{1000 K}</math> = 157 kJ/K. Im dritten, isobaren Teilprozess gibt das Helium die thermische Energie <math>W_{therm31} = n \hat c_p \Delta T = n \frac 5 2 R \Delta T</math> = 10 kmol * 2.5 * 8.31 J/K/mol * 600 K = 125 MJ ab. Diese Energie muss bei einer Temperatur von 280 K von der Entropie <math>S_{Um}=\frac{W_{therm31}}{T_{Um}}</math> = 125 MJ / 280 K = 446 kJ/K in die Umwelt hinein getragen werden. Erzeugt wird die Differenz zwischen der von Umwelt aufgenommenen und der vom Ofen abgegebenen Entropie. Diese Differenz beträgt 289 kJ/K.
+#Die total erzeugte Entropie ist die Differenz zwischen der Entropie, die im letzten Teilschritt der Umgebung zugeführt wird, und jener, die der Ofen in den beiden ersten Teilschritten abgibt. Im ersten, isochoren Teilprozess wird dem Helium die thermische Energie <math>W_{therm12} = n \hat c_V \Delta T</math> = 10 kmol * 1.5 * 8.31 J/K/mol * 600 K = 74.8 MJ zugeführt. Bei der nachfolgenden isothermen Zustandsänderung nimmt das Gas zusätzlich die thermische Energie <math>W_{therm23} = T_2 \Delta S_{23} = T_2 n R \ln{\frac{V_3}{V_2}}</math> = 900 K * 10 kmol * 8.31 J/K/mol * ln(3 m3 / 1 m3) = 82.2 MJ auf. Um die Energie für diese beiden Teilprozesse aus dem Ofen abzutransportieren, muss der Ofen die folgende Entropiemenge bei seiner konstanten Temperatur von 1000 K abgeben: <math>S_{Ofen}=\frac{W_{therm12} + W_{therm23}}{T_{Ofen}}=\frac{74.8 MJ + 82.2 MJ}{1000 K}</math> = 157 kJ/K. Im dritten, isobaren Teilprozess gibt das Helium die thermische Energie <math>W_{therm31} = n \hat c_p \Delta T = n \frac 5 2 R \Delta T</math> = 10 kmol * 2.5 * 8.31 J/K/mol * 600 K = 125 MJ ab. Diese Energie muss bei einer Temperatur von 280 K von der Entropie <math>S_{Um}=\frac{W_{therm31}}{T_{Um}}</math> = 125 MJ / 280 K = 446 kJ/K in die Umwelt hinein getragen werden. Wie oben geschrieben, wird die Differenz zwischen der von der Umwelt aufgenommenen und der vom Ofen abgegebenen Entropie erzeugt. Diese Differenz beträgt 446 kJ/K - 157 kJ/K = 289 kJ/K.
 '''[[Kreisprozess mit Helium|Aufgabe]]'''