Lösung zu Kraft auf Rohrstück: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 16. Dezember 2014, 09:23 Uhr

Bei dieser Problemstellung sollte man sowohl beim Aufstellen der Energiebilanz als auch bei der Impulsbilanz mit dem Ueberdruck arbeiten. Das heisst, dass der Referenzdruck der Umgebungsdruck ist, also ca. 10⁵ Pa.

Bezugsachse für Impuls von links nach rechts.

Die Ein- und Austrittsflächen betragen A₁ = π/4 * (0.1 m)² = 0.00785 m², A₂ = π/4 * (0.05 m)² = 0.00196 m² und der Volumen- und der Massenstrom I_V = v₂ * A₂ = 10 m/s * 0.00196 m² = 0.0196 m³/s, I_m = ρ * I_V = 1000 kg/m³ * 0.0196 m³/s = 19.6 kg/s.

1. Die Energiebilanz, das Gesetz von Bernoulli, liefert zusammen mit der Kontinuitätsgleichung

[math]p_1 + \frac {\rho}{2} v_1^2 = p_2 + \frac {\rho}{2} v_2^2[/math]

[math] v_1 A_1 = v_2 A_2, \quad v_1 = v_2 \cdot \frac {d_2^2}{d_1^2} = 10 m/s \cdot \frac {(0.05 m)^2}{(0.1 m)^2}[/math] = 2.50 m/s

den Ueberdruck p₁ beim Eintritt, wobei p₂ = 0 Pa den Ueberdruck beim Austritt darstellt.

[math] p_1 = p_2 + \frac {\rho}{2} \left(1 - \left(\frac {d_2}{d_1}\right)^4 \right) v_2^2 = 0 + \frac {1000 kg/m^3}{2} \left(1 - \left(\frac {0.05 m}{0.1 m}\right)^4 \right) (10 m/s)^2[/math] = 46.9 kPa

2. Die Impulsbilanz verlangt, dass sich die Festhaltekraft, die Überdruckkraft beim Eintritt und die beiden konvektiven Impulsströme zu Null addieren, weil der Impulsinhalt des Rohrstückes keine Änderung erfährt. Die Überdruckkraft beim Austritt ist 0, weil hier der Überdruck 0 ist. Die Impulsbilanz wenden wir auf das System Rohrstück plus Wasser an:

[math]F_A - F_{D1} + \left(- v_1 \right) \cdot I_m + v_2 \cdot (-I_m) = F_A - p_1 \cdot A_1 - \left(v_1 + v_2 \right) \cdot I_m = \dot p = 0[/math]

Zu den Vorzeichen der konvektiven Impulsströme: Beim Eintritt strömt der Massenstrom ins Systemhinein, also I_m positiv nehmen. Er trägt aber negativen Impuls ins System hinein, also muss der Geschwindigkeitsbetrag v₁ negativ genommen werden. Beim Austritt muss man I_m negativ nehmen, weil er das System verlässt. Der Impuls ist aber mit der Bezugsrichtung, also positive Geschwindigkeit.

Bei der Ein- und Austrittsfläche berechnen wir die Druckkraft nur mit dem Ueberdruck. Wenn auf der ganzen Systemgrenze nur der überall gleiche Umgebungsdruck (also der Luftdruck) herrschen würde, hätten wir eine Nettokraft von 0. Diese Kräfte können wir also in der Impulsbilanz weglassen. Wir müssen nur das berücksichtigen, was darüber hinausgeht: die mit dem Überdruck berechnete Druckkraft beim Eintritt und die Haltekraft F_A auf das Rohr.

[math]F_A = p_1 A_1 + v_1 I_m + v_2 I_m = [/math] 46.9 kPa * 0.00785 m² + 2.5 m/s * 19.6 kg/s + 10 m/s * 19.6 kg/s = 368 N + 49 N + 196 N = 613 N

Aufgabe

@@ Zeile 3: / Zeile 3: @@
+Bei dieser Problemstellung sollte man sowohl beim Aufstellen der Energiebilanz als auch bei der Impulsbilanz mit dem Ueberdruck arbeiten. Das heisst, dass der Referenzdruck der Umgebungsdruck ist, also ca. 10<sup>5</sup> Pa.
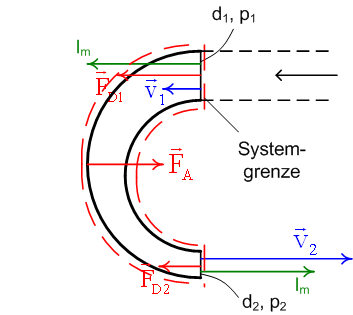
+Bezugsachse für Impuls von links nach rechts.
+Die Ein- und Austrittsflächen betragen A<sub>1</sub> = &pi;/4 * (0.1 m)<sup>2</sup> = 0.00785 m<sup>2</sup>, A<sub>2</sub> = &pi;/4 * (0.05 m)<sup>2</sup> = 0.00196 m<sup>2</sup> und der Volumen- und der [[Massenstrom]] I<sub>V</sub> = v<sub>2</sub> * A<sub>2</sub> = 10 m/s * 0.00196 m<sup>2</sup> = 0.0196 m<sup>3</sup>/s, I<sub>m</sub> = &rho; * I<sub>V</sub> = 1000 kg/m<sup>3</sup> * 0.0196 m<sup>3</sup>/s = 19.6 kg/s.
 . Die [[Energiebilanz]], das [[Gesetz von Bernoulli]], liefert zusammen mit der [[Kontinuitätsgleichung]]
-:<math>p_1 + \frac {\rho}{2} v_1^2 = p_2 + \frac {\rho}{2} v_2^2, \quad v_1 A_1 = v_2 A_2, \quad v_1 = v_2 \cdot \frac {d_2^2}{d_1^2}</math>
+:<math>p_1 + \frac {\rho}{2} v_1^2 = p_2 + \frac {\rho}{2} v_2^2</math>
+:<math> v_1 A_1 = v_2 A_2, \quad v_1 = v_2 \cdot \frac {d_2^2}{d_1^2} = 10 m/s \cdot \frac {(0.05 m)^2}{(0.1 m)^2}</math> = 2.50 m/s
+:den Ueberdruck p<sub>1</sub> beim Eintritt, wobei p<sub>2</sub> = 0 Pa den Ueberdruck beim Austritt darstellt.
+:<math> p_1 = p_2 + \frac {\rho}{2} \left(1 - \left(\frac {d_2}{d_1}\right)^4 \right) v_2^2 = 0 + \frac {1000 kg/m^3}{2} \left(1 - \left(\frac {0.05 m}{0.1 m}\right)^4 \right) (10 m/s)^2</math> =  46.9 kPa
-:den Eintrittsdruck, wobei p<sub>2</sub> = p<sub>L</sub> = 10<sup>5</sup> Pa den Luftdruck und p<sub>e</sub> = p<sub>1</sub> - p<sub>2</sub> den Ueberdruck beim Eintritt darstellt
+. Die [[Impulsbilanz]] verlangt, dass sich die Festhaltekraft, die Überdruckkraft beim Eintritt und die beiden konvektiven Impulsströme zu Null addieren, weil der Impulsinhalt des Rohrstückes keine Änderung erfährt. Die Überdruckkraft beim Austritt ist 0, weil hier der Überdruck 0 ist. Die Impulsbilanz wenden wir auf das System Rohrstück plus Wasser an:
-:<math>p_1 = p_2 + \frac {\rho}{2} \left(1 - \left(\frac {d_2}{d_1}\right)^4 \right) v_2^2</math> = p<sub>L</sub> + 46.9 kPa
+:<math>F_A - F_{D1} + \left(- v_1 \right) \cdot I_m + v_2 \cdot (-I_m) = F_A - p_1 \cdot A_1 - \left(v_1 + v_2 \right) \cdot I_m = \dot p = 0</math>
-. Die [[Impulsbilanz]] verlangt, dass sich die Festhaltekraft, die Überdruckkraft beim Eintritt und die beiden konvektiven Impulsströme zu Null addieren, weil der Impulsinhalt des Rohrstückes keine Änderung erfährt:
+Zu den Vorzeichen der konvektiven Impulsströme: Beim Eintritt strömt der Massenstrom ins Systemhinein, also I<sub>m</sub> positiv nehmen. Er trägt aber negativen Impuls ins System hinein, also muss der Geschwindigkeitsbetrag v<sub>1</sub> negativ genommen werden. Beim Austritt muss man I<sub>m</sub> negativ nehmen, weil er das System verlässt. Der Impuls ist aber mit der Bezugsrichtung, also positive Geschwindigkeit.
-:<math>F_A - p_1 A_1 - p_2 A_2 + \left(- v_1 \right) \cdot I_m + v_2 \cdot \left( -I_m\right) = \dot p = 0</math>
+Bei der Ein- und Austrittsfläche berechnen wir die Druckkraft nur mit dem Ueberdruck. Wenn auf der ganzen Systemgrenze nur der überall gleiche Umgebungsdruck (also der Luftdruck) herrschen würde, hätten wir eine Nettokraft von 0. Diese Kräfte können wir also in der Impulsbilanz weglassen. Wir müssen nur das berücksichtigen, was darüber hinausgeht: die mit dem Überdruck berechnete Druckkraft beim Eintritt und die Haltekraft F<sub>A</sub> auf das Rohr.
-:<math>F_A = (p_e + p_L) A_1 + p_L A_2 + \left(v_1 + v_2\right) I_m = p_L (A_1 + A_2) + p_e A_1 + \rho v_2 \left(\left(\frac {d_2}{d_1}\right)^2  + 1 \right) I_V</math> = 982N + 368N + 49.1N + 196.3N = 1595 N
+:<math>F_A = p_1 A_1 + v_1 I_m + v_2 I_m = </math> 46.9 kPa * 0.00785 m<sup>2</sup> + 2.5 m/s * 19.6 kg/s + 10 m/s * 19.6 kg/s = 368 N + 49 N + 196 N = 613 N
-:Der [[Massenstrom]] <math>I_m = \rho I_V = \rho A v</math> hat eine Stärke von 19.63 kg/s.
 '''[[Kraft auf Rohrstück|Aufgabe]]'''