Schraubenfeder: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:Schraubenfeder.gif|thumb|zylindrische Schraubenfeder]] Eine zylindrische Schraubendruck- oder Schraubenzugfeder verhält sich nahezu linear. Die Stärke des durchfliessenden [[Impulsstrom]]es |
[[Bild:Schraubenfeder.gif|thumb|zylindrische Schraubenfeder]] Eine zylindrische Schraubendruck- oder Schraubenzugfeder verhält sich nahezu linear. Die Stärke des durchfliessenden [[Impulsstrom]]es nimmt proportional mit der Verkürzung der Feder zu. Bezeichnet man die Stärke des hindurch fliessenden Impulsstromes etwas salopp mit ''F'' für [[Kraft]] und die Federkonstante wie im Maschinenbau üblich mit ''c'', lautet das Federgesetz |
||
:<math>F=c\Delta x</math> |
:<math>F=c\Delta x</math> |
||
| Zeile 5: | Zeile 5: | ||
''Δ x'' beschreibt die Änderung der Länge der Feder. |
''Δ x'' beschreibt die Änderung der Länge der Feder. |
||
Die mechanisch freisetzbare Energie der Feder ist gleich der [[Arbeit einer Kraft|Arbeit der Kraft]] am einen Federende, falls das andere Ende festgehalten |
Die mechanisch freisetzbare Energie der Feder ist gleich der geleisteten [[Arbeit einer Kraft|Arbeit der Kraft]] am einen Federende, falls das andere Ende bei der Verformung festgehalten worden ist. Diese Arbeit entspricht im Kraft-Verformungs-Diagramm der Fläche unter der Kurve. Somit ist die mechanisch freisetzbare Energie der Feder gleich |
||
:<math>W=\frac{c}{2}(\Delta x)^2</math> |
:<math>W=\frac{c}{2}(\Delta x)^2</math> |
||
Die Konstante ''c'' einer zylindrischen Schraubenfeder kann |
Die Konstante ''c'' einer zylindrischen Schraubenfeder kann bei bekannter Geometrie berechnet werden |
||
:<math>c=\frac{Gd^4}{8D^3N}</math> |
:<math>c=\frac{Gd^4}{8D^3N}</math> |
||
Aktuelle Version vom 28. November 2007, 07:54 Uhr
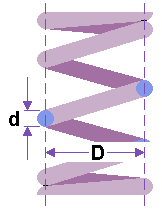
Eine zylindrische Schraubendruck- oder Schraubenzugfeder verhält sich nahezu linear. Die Stärke des durchfliessenden Impulsstromes nimmt proportional mit der Verkürzung der Feder zu. Bezeichnet man die Stärke des hindurch fliessenden Impulsstromes etwas salopp mit F für Kraft und die Federkonstante wie im Maschinenbau üblich mit c, lautet das Federgesetz
- [math]F=c\Delta x[/math]
Δ x beschreibt die Änderung der Länge der Feder.
Die mechanisch freisetzbare Energie der Feder ist gleich der geleisteten Arbeit der Kraft am einen Federende, falls das andere Ende bei der Verformung festgehalten worden ist. Diese Arbeit entspricht im Kraft-Verformungs-Diagramm der Fläche unter der Kurve. Somit ist die mechanisch freisetzbare Energie der Feder gleich
- [math]W=\frac{c}{2}(\Delta x)^2[/math]
Die Konstante c einer zylindrischen Schraubenfeder kann bei bekannter Geometrie berechnet werden
- [math]c=\frac{Gd^4}{8D^3N}[/math]
G bezeichnet das Schubmodul des verwendeten Materials. Federstahl hat ein Schubmodul von etwa 80 GPa. N steht für die Zahl der wirksamen Windungen.