Fahrwerk-Fallversuch: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
:<math>\Delta W_G+\Delta W_F=-mg(h+s_{max})+\frac 12 Ds_{max}^2=0</math> |
:<math>\Delta W_G+\Delta W_F=-mg(h+s_{max})+\frac 12 Ds_{max}^2=0</math> |
||
Die Lösung dieser Gleichung liefert einen |
Die Lösung dieser Gleichung liefert einen Federweg von |
||
:<math>s_{max}=\frac{mg}{D}+\sqrt{\left(\frac{mg}{D}\right)^2+\frac{2mgh}{D}}=\frac{mg}{D}+\sqrt{\left(\frac{mg}{D}\right)^2+\frac{mv_0^2}{D}}</math> |
:<math>s_{max}=\frac{mg}{D}+\sqrt{\left(\frac{mg}{D}\right)^2+\frac{2mgh}{D}}=\frac{mg}{D}+\sqrt{\left(\frac{mg}{D}\right)^2+\frac{mv_0^2}{D}}</math> |
||
| Zeile 24: | Zeile 24: | ||
Die Maximalbeschleunigung, die nach oben gerichtet ist, lässt sich mit Hilfe des Grundgesetzes der Mechanik ([[Impulsbilanz]]) ermitteln |
Die Maximalbeschleunigung, die nach oben gerichtet ist, lässt sich mit Hilfe des Grundgesetzes der Mechanik ([[Impulsbilanz]]) ermitteln |
||
:<math>a=\frac{F_G-F_N}{m |
:<math>a=\frac{F_G-F_N}{m}=-g\sqrt{1+\frac{2Dh}{mg}}=-g\sqrt{1+\frac{Dv_0^2}{mg^2}}</math> |
||
Ein [[Beschleunigungssensor]], der auf dem fallenden Körper montiert ist, misst zu diesem Zeitpunkt das lokal nachweisbare [[Gravitationsfeld]] der Stärke |
Ein [[Beschleunigungssensor]], der auf dem fallenden Körper montiert ist, misst zu diesem Zeitpunkt das lokal nachweisbare [[Gravitationsfeld]] der Stärke |
||
:<math>g'=g-a=g\left(1+\sqrt{1+\frac{2Dh}{mg}}\right)=g\left(1+\sqrt{1+\frac{Dv_0^2}{ |
:<math>g'=g-a=g\left(1+\sqrt{1+\frac{2Dh}{mg}}\right)=g\left(1+\sqrt{1+\frac{Dv_0^2}{mg^2}}\right)</math> |
||
Diese lokale Feldstärke zeigt gegen unten und ist um 1''g'' grösser als die Beschleunigung des Klotzes |
Diese lokale Feldstärke zeigt gegen unten und ist um 1''g'' grösser als die Beschleunigung des Klotzes. Bei einer Vertikalbewegung unterscheidet sich die Anzeige des Beschleunigungssensors immer um +/-1''g'' von der wahren Beschleunigung (Beschleunigung des Körpers gegenüber einem erdfesten Bezugssystem). |
||
==Simulationsmodell== |
==Simulationsmodell== |
||
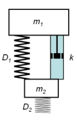
Im einfachstem Fall modelliert man das Flugzeug und die Räder je als starre Massen, das Fahrwerk als Feder-Dämpfer-System und den Pneu als reine Feder. Die Bilder zeigen das Wirkmodell sowie das [[System Dynamics|systemdynamische Modell]] ([[Systemdiagramm]]). |
|||
<gallery> |
|||
Bild:Aviatik 08 2 5.jpg|Wirkmodell |
|||
Bild:LandingGear SD.jpg|Systemdiagramm |
|||
</gallery> |
|||
[[Kategorie:Trans]] |
[[Kategorie:Trans]] |
||
Aktuelle Version vom 4. Februar 2009, 09:01 Uhr
Im Fahrwerk-Fallversuch (engl. Landing gear drop test) muss der Nachweis erbracht werden, dass das Fahrwerk eines Flugzeuges auch einen harten Landestross unbeschadet übersteht.
Versuchsanordnung
einfaches Modell
Im einfachsten Modell des fallenden Fahrwerks lässt man einen Körper (Masse m) aus einer Höhe h auf eine lineare Feder (Richtgrösse oder Federkonstante D) fallen. Dieses einfache Modell liefert eine erste Abschätzung für folgende Grössen
Federweg
Der Federweg, die maximale Verkürzung der Feder (smax), kann mit Hilfe der Energie berechnet werden
- [math]\Delta W_G+\Delta W_F=-mg(h+s_{max})+\frac 12 Ds_{max}^2=0[/math]
Die Lösung dieser Gleichung liefert einen Federweg von
- [math]s_{max}=\frac{mg}{D}+\sqrt{\left(\frac{mg}{D}\right)^2+\frac{2mgh}{D}}=\frac{mg}{D}+\sqrt{\left(\frac{mg}{D}\right)^2+\frac{mv_0^2}{D}}[/math]
wobei v0 für die Aufprallgeschwindigkeit steht.
Normalkraft und Beschleunigung
Der Maximalbetrag der Normalkraft entspricht dem durch die Feder fliessenden Impulsstrom und ist gemäss Federgesetz gleich
- [math]F_N=F_F=Ds_{max}=mg+\sqrt{\left(mg\right)^2+2Dmgh}[/math]
Die Maximalbeschleunigung, die nach oben gerichtet ist, lässt sich mit Hilfe des Grundgesetzes der Mechanik (Impulsbilanz) ermitteln
- [math]a=\frac{F_G-F_N}{m}=-g\sqrt{1+\frac{2Dh}{mg}}=-g\sqrt{1+\frac{Dv_0^2}{mg^2}}[/math]
Ein Beschleunigungssensor, der auf dem fallenden Körper montiert ist, misst zu diesem Zeitpunkt das lokal nachweisbare Gravitationsfeld der Stärke
- [math]g'=g-a=g\left(1+\sqrt{1+\frac{2Dh}{mg}}\right)=g\left(1+\sqrt{1+\frac{Dv_0^2}{mg^2}}\right)[/math]
Diese lokale Feldstärke zeigt gegen unten und ist um 1g grösser als die Beschleunigung des Klotzes. Bei einer Vertikalbewegung unterscheidet sich die Anzeige des Beschleunigungssensors immer um +/-1g von der wahren Beschleunigung (Beschleunigung des Körpers gegenüber einem erdfesten Bezugssystem).
Simulationsmodell
Im einfachstem Fall modelliert man das Flugzeug und die Räder je als starre Massen, das Fahrwerk als Feder-Dämpfer-System und den Pneu als reine Feder. Die Bilder zeigen das Wirkmodell sowie das systemdynamische Modell (Systemdiagramm).
-
Wirkmodell
-
Systemdiagramm