Lösung zu Mantelstromtriebwerk: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 4. März 2010, 17:54 Uhr

Die Impulsbilanz bezüglich des Triebwerkes lautet unter Vernachlässigung der Druckkräfte, bei stationärem Betrieb und mit Bezugsrichtung = Flugrichtung

[math]-F_F + I_{mi} \cdot (-v_i) - I_{mD} \cdot (-v_D) - I_{mM} \cdot (-v_M) = \dot p = 0[/math],

wobei für die Geschwindigkeiten die Beträge eingesetzt werden und der durchgepumpte Massenstrom die folgende Stärke aufweist

[math]I_{mi} = \rho v_i A_i[/math] = 0.85 kg/m³ * 250 m/s * π/4 * (2 m)² = 667.6 kg/s.

Die Kraft des Flugzeug auf das Triebwerk F_F weist gegen hinten, die zugehörige Reaktionskraft auf das Flugzeug, der Schub, gegen vorne. Die Impulsänderungsrate ist 0 wegen des stationären Betriebs. Mit v_D = 2 * v_i, v_M = 1.25 * v_i, I_mD = 0.2 * I_mi und I_mM = 0.8 * I_mi ergibt das:

[math]-F_F - I_{mi} \cdot v_i + 0.2 \cdot I_{mi} \cdot 2 \cdot v_i + 0.8 \cdot I_{mi} \cdot 1.25 \cdot v_i = 0[/math]

Damit erhält man für die Schubkraft

[math]F_{Schub} = F_F = 0.4 \cdot v_i \cdot I_{mi}[/math] = 66.76 kN

Aufgabe

@@ Zeile 1: / Zeile 1: @@
 [[Bild:Mantelstromtriebwerk.png]]
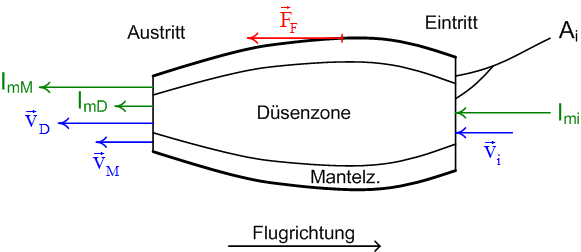
-Die Impulsbilanz bezüglich des Triebwerkes lautet unter Vernachlässigung der Druckkräfte
+Die Impulsbilanz bezüglich des Triebwerkes lautet unter Vernachlässigung der Druckkräfte, bei stationärem Betrieb und mit Bezugsrichtung = Flugrichtung
+:<math>-F_F + I_{mi} \cdot (-v_i) - I_{mD} \cdot (-v_D) - I_{mM} \cdot (-v_M) = \dot p = 0</math>,
+wobei für die Geschwindigkeiten die Beträge eingesetzt werden und der durchgepumpte Massenstrom die folgende Stärke aufweist
-:<math>F_F + v_i I_{mi} + v_D I_{mD} + v_M I_{mM} = \dot p = 0</math>
+:<math>I_{mi} = \rho v_i A_i</math> = 0.85 kg/m<sup>3</sup> * 250 m/s * &pi;/4 * (2 m)<sup>2</sup> = 667.6 kg/s.
-wobei der durchgepumpte Massenstrom die folgende Stärke aufweist
+Die Kraft des Flugzeug auf das Triebwerk '''''F<sub>F</sub>''''' weist gegen hinten, die zugehörige Reaktionskraft auf das Flugzeug, der Schub, gegen vorne. Die Impulsänderungsrate ist 0 wegen des stationären Betriebs. Mit v<sub>D</sub> = 2 * v<sub>i</sub>, v<sub>M</sub> = 1.25 * v<sub>i</sub>, I<sub>mD</sub> = 0.2 * I<sub>mi</sub>  und I<sub>mM</sub> = 0.8 * I<sub>mi</sub> ergibt das:
-:<math>I_{mi} = \rho v_i A_i</math> = 667.6 kg/s.
+:<math>-F_F - I_{mi} \cdot v_i + 0.2 \cdot I_{mi} \cdot 2 \cdot v_i + 0.8 \cdot I_{mi} \cdot 1.25 \cdot v_i = 0</math>
-Die Kraft des Flugzeug auf das Triebwerk '''''F<sub>F</sub>''''' weist gegen hinten, die zugehörige Reaktionskraft auf das Flugzeug, der Schub, gegen vorne. Die Impulsänderungsrate ist 0, weil sich das Triebwerk im gewählten Bezugssystem nicht bewegt. Das ist nur dann richtig, wenn die Geschwindigkeit des Flugzeug konstant ist. Bei positiver Beschleunigung a entsteht eine nach hinten gerichtete Trägheitskraft <math>F_t = m g_t = - m a = \dot p</math>. Diese ist also gerade gleich gross wie die Impulsänderungsrate, sodass sich in der Impulsbilanz netto nichts ändert.
-Da alle Geschwindigkeiten, aber nur die austretenden Massenströme negativ sind, bleiben deren Produkte positiv:
-:<math>F_F - v_i \cdot I_{mi} + 2 v_i \cdot \frac {1}{5} I_{mi} + \frac {5}{4} v_i \cdot \frac {4}{5} I_{mi} = 0</math>
 Damit erhält man für die Schubkraft
-:<math>F_{Schub} = -F_F = \frac {2}{5} v_i \cdot I_{mi}</math> = 66.76 kN
+:<math>F_{Schub} = F_F = 0.4 \cdot v_i \cdot I_{mi}</math> = 66.76 kN