Lösung zu Kreisprozess dreiteilig: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 10. April 2010, 17:13 Uhr

T-S-Diagramm
p-V-Diagramm

Im T-S-Diagramm verläuft die isochore Zustandsänderung exponentiell, die isentrope vertikal und die isotherme horizontal. Im p-V-Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf der [math]pV^k=p_0V_0^k[/math] - Kurve nach rechts unten und auf einer Hyperbel wieder nach links oben. Im T-S-Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. Im p-V-Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit.
Die innere Energie eines idealen Gases hängt nur von der Temperatur ab. Im ersten Teilprozess (isochor) nimmt die innere Energie um [math]\Delta W_1 = n \hat c_V \Delta T = n \frac 3 2 R\Delta T[/math] = 50 mol * 1.5 * 8.31 J/K/mol * 300 K = 187 kJ zu. Um genau diesen Betrag nimmt die innere Energie im zweiten, isentropen Prozess wieder ab, weil das Gas wieder auf die Anfangstemperatur zurückgebracht wird: ΔW₂ = - 187 kJ. Im 3. Teilprozess ändert sich die innere Energie nicht mehr, weil die Temperatur konstant bleibt: ΔW₃ = 0.
Im ersten Teilprozess nimmt die Entropie um [math]\Delta S_1=n\hat c_V\ln{\frac{T_2}{T_1}}=n\frac 3 2 R\ln{\frac{T_2}{T_1}}[/math] = 50 mol * 1.5 * 8.31 J/K/mol * ln(500 K / 200 K) = 571 J/K zu. Im zweiten, isentropen Teilprozess bleibt die Entropie konstant. Und im dritten, isothermen Teilprozess, der das Gas wieder auf die Anfangstemperatur zurückbringt, nimmt sie um denselben Betrag wieder ab wie im ersten Teilprozess: ΔS₃ = - 571 J/K.
Die Arbeit, also die mechanisch abgegebene Energie, entspricht der Fläche, die vom Prozess im p-V-Diagramm eingeschlossen wird. Während des ersten Teilprozesses ist die Arbeit 0, weil sich das Volumen nicht ändert: W_mech,1 = 0. Im zweiten, isentropen Teilprozess ist die mechanisch abgeführte Energie gleich der Änderung der inneren Energie, weil keine thermische Energie ausgetauscht wird: W_mech,2 = ΔW₂ = - 187 kJ. Im dritten Teilprozess ändert sich die innere Energie nicht: ΔW₃ = W_mech,3 + W_therm,3 = 0. Deshalb ist die thermisch abgegebene Energie gleich der mechanisch zugeführten: W_mech,3 = - W_therm,3. Die thermisch abgeführte Energie können wir mit der abgeführten Entropie und der konstanten Temperatur berechnen: W_mech,3 = - W_therm,3 = - (- 571 J/K) * 200 K = 114 kJ. Die Kompressionsarbeit beträgt demnach 114 kJ. Durch Addition aller Arbeiten erhält man für den ganzen Zyklus eine mechanisch abgeführte Energie von W_mech,Prozess = W_mech,1 + W_mech,2 + W_mech,3 = - 187 kJ + 0 + 114 kJ = - 73 kJ.

Aufgabe

@@ Zeile 4: / Zeile 4: @@
 </gallery>
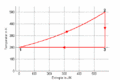
-#Im ''T-S-''Diagramme verläuft die isochore Zustandsänderung exponentiell, die isentrope vertikal und die isotherme horizontal. Im ''p-V-''Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf der <math>pV^k=p_0V_0^k</math> - Kurve nach rechts unten und auf einer Hyperbel wieder nach links oben. Im ''T-S-''Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. 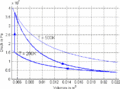Im ''p-V-''Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit.
+#Im ''T-S-''Diagramm verläuft die isochore Zustandsänderung exponentiell, die isentrope vertikal und die isotherme horizontal. Im ''p-V-''Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf der <math>pV^k=p_0V_0^k</math> - Kurve nach rechts unten und auf einer Hyperbel wieder nach links oben. Im ''T-S-''Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. Im ''p-V-''Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit.
-#Die [[innere Energie]] eines Gases hängt nur von der Temperatur ab. Im ersten Teilprozess (isochor) nimmt die innere Energie um <math>\Delta W=n\hat c_V\Delta T=\frac 3 2 nR\Delta T</math> = 187 kJ zu. Um genau diesen Betrag nimmt die innere Energie im zweiten, isentropen Prozess wieder ab.
+#Die [[innere Energie]] eines idealen Gases hängt nur von der Temperatur ab. Im ersten Teilprozess (isochor) nimmt die innere Energie um <math>\Delta W_1 = n \hat c_V \Delta T = n \frac 3 2 R\Delta T</math> = 50 mol * 1.5 * 8.31 J/K/mol * 300 K = 187 kJ zu. Um genau diesen Betrag nimmt die innere Energie im zweiten, isentropen Prozess wieder ab, weil das Gas wieder auf die Anfangstemperatur zurückgebracht wird: &Delta;W<sub>2</sub> = - 187 kJ. Im 3. Teilprozess ändert sich die innere Energie nicht mehr, weil die Temperatur konstant bleibt: &Delta;W<sub>3</sub> = 0.
-#Im ersten Prozess nimmt die Entropie um <math>\Delta S=n\hat c_V\ln{\frac{T_2}{T_1}}=\frac 3 2 nR\ln{\frac{T_2}{T_1}}</math> = 571 J/K zu. Diese Entropie wird im dritten Teilprozess isotherm an die Umgebung abgegeben.
+#Im ersten Teilprozess nimmt die Entropie um <math>\Delta S_1=n\hat c_V\ln{\frac{T_2}{T_1}}=n\frac 3 2 R\ln{\frac{T_2}{T_1}}</math> = 50 mol * 1.5 * 8.31 J/K/mol * ln(500 K / 200 K)  = 571 J/K zu. Im zweiten, isentropen Teilprozess bleibt die Entropie konstant. Und im dritten, isothermen Teilprozess, der das Gas wieder auf die Anfangstemperatur zurückbringt, nimmt sie um denselben Betrag wieder ab wie im ersten Teilprozess: &Delta;S<sub>3</sub> = - 571 J/K.
-#Im isentropen Teilprozess ist die mechanisch abgeführten Energie gleich der Änderung der inneren Energie. Folglich ist die Arbeit gleich -187 kJ. Weil sich im dritten Teilprozess die innere Energie nicht ändert, ist die thermisch abgegebene Energie gleich der mechanisch zugeführten. Die thermisch abgeführte Energie ist gleich abgeführte Entropie mal herrschende Temperatur, also gleich -571 J/K * 200 K = -114 kJ. Die Kompressionsarbeit beträgt demnach 114 kJ. Durch Addition der beiden Arbeiten erhält man für den ganzen Zyklus eine mechanisch abgeführte Energie von -73 kJ.
+#Die Arbeit, also die mechanisch abgegebene Energie, entspricht der Fläche, die vom Prozess im p-V-Diagramm eingeschlossen wird. Während des ersten Teilprozesses ist die Arbeit 0, weil sich das Volumen nicht ändert: W<sub>mech,1</sub> = 0. Im zweiten, isentropen Teilprozess ist die mechanisch abgeführte Energie gleich der Änderung der inneren Energie, weil keine thermische Energie ausgetauscht wird: W<sub>mech,2</sub> = &Delta;W<sub>2</sub> = - 187 kJ. Im dritten Teilprozess ändert sich die innere Energie nicht: &Delta;W<sub>3</sub> = W<sub>mech,3</sub> + W<sub>therm,3</sub> = 0. Deshalb ist die thermisch abgegebene Energie gleich der mechanisch zugeführten: W<sub>mech,3</sub> = - W<sub>therm,3</sub>. Die thermisch abgeführte Energie können wir mit der abgeführten Entropie und der konstanten Temperatur berechnen: W<sub>mech,3</sub> = - W<sub>therm,3</sub> = - (- 571 J/K) * 200 K = 114 kJ. Die Kompressionsarbeit beträgt demnach 114 kJ. Durch Addition aller Arbeiten erhält man für den ganzen Zyklus eine mechanisch abgeführte Energie von W<sub>mech,Prozess</sub> = W<sub>mech,1</sub> + W<sub>mech,2</sub> + W<sub>mech,3</sub> = - 187 kJ + 0 + 114 kJ = - 73 kJ.
 '''[[Kreisprozess dreiteilig|Aufgabe]]'''