Lösung zu Luftspeicher: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) (Die Seite wurde neu angelegt: #Im ''T-S-''Diagramm bilden die Isentropen vertikale Linien, die Isochoren verlaufen exponentiell in Funktion der Entropie oder logarithmisch mit der Temperatur. Im ''p...) |
Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<gallery> |
|||
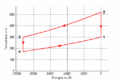
Bild:Luftspeicher T-S Diagramm.gif|''T-S-''Diagramm |
|||
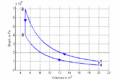
Bild:Luftspeicher p-V-Diagramm.gif|''p-V-''Diagramm |
|||
</gallery> |
|||
#Im ''T-S-''Diagramm bilden die Isentropen vertikale Linien, die Isochoren verlaufen exponentiell in Funktion der Entropie oder logarithmisch mit der Temperatur. Im ''p-V-''Diagramm schneiden die Isentropen die Isothermen unter einem spitzen Winkel, die Isochoren verlaufen vertikal. |
#Im ''T-S-''Diagramm bilden die Isentropen vertikale Linien, die Isochoren verlaufen exponentiell in Funktion der Entropie oder logarithmisch mit der Temperatur. Im ''p-V-''Diagramm schneiden die Isentropen die Isothermen unter einem spitzen Winkel, die Isochoren verlaufen vertikal. |
||
#Am Ende des ersten |
#Am Ende des ersten Teilprozesses beträgt der Druck <math>p_2=p_1\left(\frac {V_1}{V_2}\right)^\kappa</math> = 1 bar * (20 m<sup>3</sup> / 5 m<sup>3</sup>)<sup>1.4</sup> = 6.96 bar und die Temperatur ist gleich <math>T_2=T_1\frac{p_2V_2}{p_1 V_1}</math> = 300 K * (6.96 bar * 5 m<sup>3</sup>)/(1 bar * 20 m<sup>3</sup>) = 522 K. Nach dem zweiten Teilprozess betragen das Volumen V<sub>3</sub> = 5 m<sup>3</sup>, die Temperatur T<sub>3</sub> = 300 K und der Druck p<sub>3</sub> = p<sub>1</sub> * V<sub>1</sub> / V<sub>3</sub> = 1 bar * 20 m<sup>3</sup> / 5 m<sup>3</sup> = 4 bar. Nach dem dritten Teilprozess beträgt der Druck nur noch <math>p_4 = p_3\left(\frac {V_3}{V_4}\right)^\kappa</math> = 4 bar * (5 m<sup>3</sup> / 20 m<sup>3</sup>)<sup>1.4</sup> = 0.574 bar und die Temperatur misst <math>T_4 = T_3 \frac{p_4 V_4}{p_3 V_3}</math> = 300 K * (0.574 bar * 20 m<sup>3</sup>)/(4 bar * 5 m<sup>3</sup>) = 172 K. Für die Berechnung dieser Werte geht man am besten vom Anfangszustand des isentropen Teilprozesses aus und verwendet dann die Isentropengleichung und die thermische Zustandsgleichung. |
||
#Die Arbeit bei den isochoren Teilprozessen ist 0. Weil bei den isentropen Teilprozessen keine thermische Energie ausgetauscht wird, ist dabei die Arbeit gleich der Änderung der inneren Energie. Diese hängt wiederum nur von der Temperatur ab: <math> W_{mech, netto} = \Delta W_{12} + \Delta W_{34} = n \hat c_V (T_2-T_1+T_4-T_3) </math> = 802 mol * 2.5 * 8.31 J/K/mol * (522 K - 300 K + 172 K - 300 K) = 1.57 MJ. Die Stoffmenge berechnet man aus den Anfangswerten: <math>n = \frac {p_1 V_1}{R T_1}</math> = 1 bar * 20 m<sup>3</sup> / 8.31 J/K/mol / 300 K = 802 mol. |
|||
#Im zweiten Teilprozess, der isochoren Auskühlung, beträgt die Änderung der inneren Energie <math>\Delta W=n\hat c_V(T_3-T_2)</math> = 802 mol * 2.5 * 8.31 J/K/mol * (300 K - 522 K) = - 3.70 MJ. Die zugehörige Entropieänderung ist gleich <math>\Delta S=n\hat c_V\ln\left(\frac{T_3}{T_2}\right)</math> = 802 mol * 2.5 * 8.31 J/K/mol * ln(300 K / 522 K) = - 9.23 kJ/K. |
|||
'''[[Luftspeicher|Aufgabe]]''' |
|||
Aktuelle Version vom 13. April 2010, 14:45 Uhr
-
T-S-Diagramm
-
p-V-Diagramm
- Im T-S-Diagramm bilden die Isentropen vertikale Linien, die Isochoren verlaufen exponentiell in Funktion der Entropie oder logarithmisch mit der Temperatur. Im p-V-Diagramm schneiden die Isentropen die Isothermen unter einem spitzen Winkel, die Isochoren verlaufen vertikal.
- Am Ende des ersten Teilprozesses beträgt der Druck [math]p_2=p_1\left(\frac {V_1}{V_2}\right)^\kappa[/math] = 1 bar * (20 m3 / 5 m3)1.4 = 6.96 bar und die Temperatur ist gleich [math]T_2=T_1\frac{p_2V_2}{p_1 V_1}[/math] = 300 K * (6.96 bar * 5 m3)/(1 bar * 20 m3) = 522 K. Nach dem zweiten Teilprozess betragen das Volumen V3 = 5 m3, die Temperatur T3 = 300 K und der Druck p3 = p1 * V1 / V3 = 1 bar * 20 m3 / 5 m3 = 4 bar. Nach dem dritten Teilprozess beträgt der Druck nur noch [math]p_4 = p_3\left(\frac {V_3}{V_4}\right)^\kappa[/math] = 4 bar * (5 m3 / 20 m3)1.4 = 0.574 bar und die Temperatur misst [math]T_4 = T_3 \frac{p_4 V_4}{p_3 V_3}[/math] = 300 K * (0.574 bar * 20 m3)/(4 bar * 5 m3) = 172 K. Für die Berechnung dieser Werte geht man am besten vom Anfangszustand des isentropen Teilprozesses aus und verwendet dann die Isentropengleichung und die thermische Zustandsgleichung.
- Die Arbeit bei den isochoren Teilprozessen ist 0. Weil bei den isentropen Teilprozessen keine thermische Energie ausgetauscht wird, ist dabei die Arbeit gleich der Änderung der inneren Energie. Diese hängt wiederum nur von der Temperatur ab: [math] W_{mech, netto} = \Delta W_{12} + \Delta W_{34} = n \hat c_V (T_2-T_1+T_4-T_3) [/math] = 802 mol * 2.5 * 8.31 J/K/mol * (522 K - 300 K + 172 K - 300 K) = 1.57 MJ. Die Stoffmenge berechnet man aus den Anfangswerten: [math]n = \frac {p_1 V_1}{R T_1}[/math] = 1 bar * 20 m3 / 8.31 J/K/mol / 300 K = 802 mol.
- Im zweiten Teilprozess, der isochoren Auskühlung, beträgt die Änderung der inneren Energie [math]\Delta W=n\hat c_V(T_3-T_2)[/math] = 802 mol * 2.5 * 8.31 J/K/mol * (300 K - 522 K) = - 3.70 MJ. Die zugehörige Entropieänderung ist gleich [math]\Delta S=n\hat c_V\ln\left(\frac{T_3}{T_2}\right)[/math] = 802 mol * 2.5 * 8.31 J/K/mol * ln(300 K / 522 K) = - 9.23 kJ/K.