Kraftfluss: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
(→Links) |
||
| (22 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Begriff== |
==Begriff== |
||
"Unter dem Kraftfluss versteht man den Weg einer Kraft und/oder eines Moments in einem Bauteil vom Angriffspunkt (Stelle der Einleitung!) bis zur Stelle, an der diese durch eine Reaktionskraft und/oder ein Reaktionsmoment aufgenommen werden" (Quelle: Vorlesungsunterlagen 2002, ''Prof. Dr.-Ing. Dr. h. c. mult. Uwe Heisel'', Institut für Werkzeugmaschinen, Uni Stuttgart) |
|||
"Bei der Erarbeitung massstäblicher Entwürfe stellt sich dem Konstrukteur vielfach die Aufgabe, für eine optimale Leitung von Kräften, Drehmomenten und/oder Biegemomenten durch die vorgesehenen Funktionsträger sorgen zu müssen. Zur Veranschaulichung der Funktion '''Leiten von Kräften und Momenten''' wird gern der Begriff '''Kraftfluss''' verwendet." (Quelle: ''Hintzen H., Laufenberg H.'':Konstruieren und Berechnen, Vieweg) |
|||
"Kraftfluss, Kraftleitung: äussere Lasten bewirken Schnittgrössen, die Beanspruchungen (Kräfte, Momente) hervorrufen, welche eleastische oder plastische Verformung hervorrufen." (Quelle: Vorlesungsunterlagen SS 2004 ''Prof. Dr. Ing. Lucienne Biessing'') |
|||
==Theoretische Grundlagen== |
==Theoretische Grundlagen== |
||
In der Punktmechanik kennt man nur Körper und Kräfte, welche zwischen den Körpern wechselwirken. Der Begriff der Kraftleitung ist erst in der [[technische Mechanik|technischen Mechanik]] aufgetaucht, als man mit Hilfe des Schnittprinzips die Konzepte der Newtonschen Punktmechanik und der Eulerschen Starrkörpermechanik auf ausgedehnte Systeme mit einer inneren Struktur übertragen hat. |
In der Punktmechanik kennt man nur Körper und Kräfte, welche zwischen den Körpern wechselwirken. Der Begriff der Kraftleitung ist erst in der [[technische Mechanik|technischen Mechanik]] aufgetaucht, als man mit Hilfe des [[Schnittprinzip|Schnittprinzips]] die Konzepte der [[Newtonsche Axiome|Newtonschen]] [[Punktmechanik]] und der Eulerschen [[starrer Körper|Starrkörpermechanik]] auf ausgedehnte Systeme mit einer inneren Struktur übertragen hat. |
||
Zur Beschreibung der Mechanik benötigt man neben der Energie sechs mengenartige oder bilanzierfähige Grössen, die drei Komponenten des Impulses und des Drehimpulses (Nöthersches Theorem). Treten diese sechs Grössen über die materielle Oberfläche eines Körpers, nennt man die zugehörigen Stromstärken '''Kraft''' oder '''Drehmoment'''. Die drei Kraftkomponenten transformieren sich wie ein Vektor, die drei Komponenten des Drehmomentes wie die drei unabhängigen Komponenten eines schiefsymmetrischen [[Tensor|Tensors]]. Solange man nur eigentliche Transformationen untersucht, verhält sich auch das Drehmoment wie ein Vektor. |
Zur Beschreibung der Mechanik benötigt man neben der Energie sechs mengenartige oder bilanzierfähige Grössen, die drei Komponenten des Impulses und des Drehimpulses (Nöthersches Theorem). Treten diese sechs Grössen über die materielle Oberfläche eines Körpers, nennt man die zugehörigen Stromstärken '''Kraft''' oder '''Drehmoment'''. Die drei Kraftkomponenten transformieren sich wie ein Vektor, die drei Komponenten des Drehmomentes wie die drei unabhängigen Komponenten eines schiefsymmetrischen [[Tensor|Tensors]]. Solange man nur eigentliche Transformationen untersucht, verhält sich auch das Drehmoment wie ein Vektor. |
||
| Zeile 17: | Zeile 17: | ||
==Impulsstrom== |
==Impulsstrom== |
||
===induzierte Wirbelströme=== |
===induzierte Wirbelströme=== |
||
Impuls wird konvektiv und leitungsartig durch den Raum transportiert. Der |
[[Impuls]] wird konvektiv und leitungsartig durch den Raum transportiert. Der [[konvektiv]]e Transport, der nur bei Flüssigkeiten und Gasen auftritt, soll hier nicht weiter thematisiert werden. Zur Darstellung des leitungsartigen Impulsstromes nimmt man die Spalten des Spannungstensors, multipliziert diese mit minus eins und zeichnet sie als je einen Pfeil in drei verschiedene Bilder ein. Impulsstrombilder lassen sich problemlos mit Femlab erzeugen. Zu beachten ist, dass die konkrete Gestalt der drei Strombilder von der Wahl des Koordinatensystems abhängt. |
||
[[Bild:Kraftfluss_Blech.gif|thumb|x- und y-Impulsstrom in einem Stück Blech]] |
[[Bild:Kraftfluss_Blech.gif|thumb|x- und y-Impulsstrom in einem Stück Blech]] |
||
| Zeile 39: | Zeile 39: | ||
===Impulsquellen=== |
===Impulsquellen=== |
||
[[Bild:Kraftfluss_Schrägseilbrücke.gif|thumb|x- und y-Impulsstrom in einem geschlossenen Bügel]] |
[[Bild:Kraftfluss_Schrägseilbrücke.gif|thumb|x- und y-Impulsstrom in einem geschlossenen Bügel]] |
||
In der Statik bilden Impulsströme über mehrere Bauteile Kreise und in den einzelnen Bauteilen Wirbel aus. Nur die Gravitationskraft vermag diese Kreisströme aufzubrechen. Die Gravitationskraft steht für den volumenmäßigen Impulsaustausch zwischen Körper und Gravitationsfeld. Zeigt die positive z-Achse nach unten, besitzt jeder Körper eine z-Impulsquelle. Diese Quelle verteilt sich über das ganze Volumen. Die Quellendichte ist gleich Massendichte mal Gravitationsfeldstärke. Das Bild zeigt die Impulsströme in einer [[Brücke|Schrägseilbrücke]]. Der z-Impuls, der vom Gravitationsfeld her zuströmt, wird über die Seile schief nach oben an die Pylone abgeführt. In den schief stehenden Seilen strömt zusätzlich noch Impuls der x-Komponente. |
In der Statik bilden Impulsströme über mehrere Bauteile Kreise und in den einzelnen Bauteilen Wirbel aus. Nur die Gravitationskraft vermag diese Kreisströme aufzubrechen. Die Gravitationskraft steht für den volumenmäßigen Impulsaustausch zwischen Körper und Gravitationsfeld. Zeigt die positive z-Achse nach unten, besitzt jeder Körper eine z-Impulsquelle. Diese Quelle verteilt sich über das ganze Volumen. Die [[Quellenstärke|Quellendichte]] ist gleich Massendichte mal Gravitationsfeldstärke. Das Bild zeigt die [[Impulsstrom|Impulsströme]] in einer [[Brücke|Schrägseilbrücke]]. Der z-Impuls, der vom Gravitationsfeld her zuströmt, wird über die Seile schief nach oben an die Pylone abgeführt. In den schief stehenden Seilen strömt zusätzlich noch Impuls der x-Komponente. |
||
In der Dynamik muss das Impulsspeichervermögen der einzelnen Körper konsistent mit den zugehörigen Strömen, den Kräften, verknüpft werden. Weil sich die träge [[Masse]] nicht von der schweren Masse unterscheidet, erzeugen beschleunigte Körper die gleichen Impulsströme wie ruhende Körper im entsprechenden Gravitationsfeld. Ein Impulsstrom kann also sowohl von einer Änderungsrate des Impulsinhaltes als auch von einem Gravitationsfeld gespiesen werden. Diese doppelte Wirkung der Masse, einmal als Impulskapazität und einmal als Teil der Quellenstärke, schafft große Verständnisprobleme in Bezug auf den Kraftbegriff. Erschwerend kommt hinzu, dass in der technischen Mechanik der Bergriff der Trägheitskraft nach d’Alambert dazu benutzt wird, ein dynamisches Problem auf ein statisches zurückzuführen, in der Physik Trägheitskräfte aber nur dann eingeführt werden, wenn das Beobachtersystem im Sinne von Newton und Mach nichtinertial ist. |
In der Dynamik muss das Impulsspeichervermögen der einzelnen Körper konsistent mit den zugehörigen Strömen, den Kräften, verknüpft werden. Weil sich die träge [[Masse]] nicht von der schweren Masse unterscheidet, erzeugen beschleunigte Körper die gleichen Impulsströme wie ruhende Körper im entsprechenden [[Gravitationsfeld]]. Ein [[Impulsstrom]] kann also sowohl von einer [[Änderungsrate]] des Impulsinhaltes als auch von einem Gravitationsfeld gespiesen werden. Diese doppelte Wirkung der Masse, einmal als Impulskapazität und einmal als Teil der Quellenstärke, schafft große Verständnisprobleme in Bezug auf den Kraftbegriff. Erschwerend kommt hinzu, dass in der technischen Mechanik der Bergriff der Trägheitskraft nach d’Alambert dazu benutzt wird, ein dynamisches Problem auf ein statisches zurückzuführen, in der Physik Trägheitskräfte aber nur dann eingeführt werden, wenn das Beobachtersystem im Sinne von Newton und Mach nichtinertial ist. |
||
==Drehimpulsstrom== |
==Drehimpulsstrom== |
||
Der [[Drehimpuls]] darf wie jede andere mengenartige Größe bezüglich eines Systems bilanziert werden. Nur sind beim Drehimpuls weder Inhalt noch Stromstärke direkt messbar. Dass diese Einschränkung den Wert des Bilanzierens nicht zu schmälern vermag, zeigt sich schon bei der [[Energie]]. Viele Fragestellungen der Mechanik lassen sich mit Hilfe der Energie lösen, obwohl weder der Energietransport noch der Energieinhalt direkt gemessen werden können. Wenn nachfolgend von Drehimpulsinhalt oder [[Drehimpulsstrom]] die Rede ist, wird nicht behauptet, dass diese Größe in jedem Fall lokalisierbar sei. Zudem hängt der konkrete Wert des Drehimpulsinhalts oder des Drehimpulsstromes von der Wahl des Koordinatensystems ab. |
|||
===Bedingte Lokalisierbarkeit=== |
|||
Üblicherweise schreibt man einer Punktmasse einen Drehimpuls bezüglich eines raumfesten Referenzpunktes zu. Entsprechend verfährt man mit dem Drehmoment. Der Drehimpuls ist so gesehen eine nichtlokale Erhaltungsgröße, deren absoluter Wert von der Lage des Bezugspunktes abhängt. Erst mit der Physik des 20. Jahrhunderts hat sich der Eigendrehimpuls unter dem Namen Spin zu einer Größe gewandelt, die wie die elektrische Ladung oder die Masse direkt einem System zugeschrieben wird. |
|||
Die bedingte Lokalisierbarkeit ist einer der Gründe, weshalb der Drehimpuls kaum als bilanzierfähige Größe wahrgenommen wird. Für den Drehimpuls kann weder eine direkt messbare Dichte noch eine lokal nachweisbare Stromdichte definiert werden. Die Bilanzgleichung leitet sich folglich nicht wie bei der elektrischen Ladung oder beim Impuls aus der [[Kontinuitätsgleichung]] ab. |
|||
===Drehimpulsströme=== |
|||
[[Bild:Bohrmaschine.jpg|thumb|Drehimpulsstrom in einer Ständerbohrmaschine]] |
|||
Ein raumfestes Koordinatensystem zerlegt den Drehimpuls in seine drei Komponenten. Jede der drei Drehimpulskomponenten kann in die eigene Bezugsrichtung oder seitwärts dazu transportiert werden. Drehimpulsströme sind aber nur mittelbar, über die sie begleitenden Impulsströme nachweisbar. Fließt der Drehimpuls in seine eigene Bezugsrichtung durch ein Bauteil, liegt Torsion vor. Bei einem Transport seitwärts zu Bezugsrichtung erleidet das Bauteil Biegung. Biegung und Torsion sind somit direkte Auswirkungen eines Drehimpulstransports. |
|||
Diese einfache Zuordnung zwischen Drehimpulstransport und Bauteilreaktion kommt der Idee eines makroskopischen Kraftflusses schon ziemlich nahe. Betrachten wir dazu eine Ständerbohrmaschine. Der z-Drehimpuls, der im Bohrer vorwärts fließt, bildet über Tisch, Säule, Halterung, Motor und Spindel einen Kreisstrom. In der Säule, in der Spindel und im Bohrer erzeugt der Drehimpulsstrom Torsion, in den Halterungen für Tisch und Motor herrscht Biegung. In diesem Beispiel ist der „Kraftfluss“ ein Drehimpulsstrom, dessen Stärke je nach Transportrichtung als Torsions- oder Biegemoment bezüglich einer Schnittebene bestens bekannt ist. |
|||
Die bildhafte Darstellung des Drehimpulses reicht weit über die Konkretisierung des Kraftflusses hinaus. Eine mit Hilfe des Drehimpulses entwickelte Rotationsmechanik lässt sich problemlos in die allgemeine Systemtheorie einbetten. Mit der Winkelgeschwindigkeit als Potenzialgröße kann jedem Drehimpulsstrom ein [[zugeordneter Energiestrom|Energiestrom]] zugeordnet werden. Torsionsfedern werden so zu [[induktives Gesetz|Induktivitäten]], Massenträgheitsmomente zu [[kapazitives Gesetz|Kapazitäten]] und Reibflächen zu (nichtlinearen) [[resistives Gesetz|Widerständen]]. In der Ständerbohrmaschine wird der Drehimpulsstrom im Elektromotor mit Energie beladen. Diese Energie setzt der Drehimpulsstrom zwischen Schnittfläche und Span wieder frei. |
|||
===Biegung=== |
|||
[[Bild:Biegespannung.gif|thumb|Impuls- und Drehimpulsstromdichte in einem gebogenen H-Balken]] |
|||
Bei Biegung wird der im Balken seitwärts fließende Drehimpulsstrom beidseits von einem Impulsstrom begrenzt. Die Impulsstromdichte ist gleich dem Gradienten der Drehimpulsstromdichte normal zur Transport- und normal zur Bezugsrichtung der Drehimpulskomponente. Die Skizze zeigt das Impuls- und Drehimpulsstromdichteprofil quer zum gebogenen Balken. Die rote Linien beziehen sich auf die Verhältnisse im Steg, die grünen Linien beschreiben die Stromdichten längs einer Linie, welche nur die Gurten normal durchstösst. Die konkrete Gestalt der Impulsstromdichte, die Verteilung der Zug- und Druckspannungen, hängt von den Materialeigenschaften ab. Die Drehimpulsstromdichte ist dann aber nur noch von der Impulsstromdichte abhängig. |
|||
Bei der reinen Biegung wird Drehimpuls seitwärts zur Definitionsrichtung transportiert. Der Drehimpulstransport wird beidseits von einem Impulsstrom begrenzt, wobei die Impulsstromdichte gleich der Änderung der Drehimpulsstromdichte normal zu den Definitionsrichtungen von Impuls und Drehimpuls ist. Weil der Impuls in oder gegen seine eigene Bezugsrichtung fließt, erzeugt er Druck oder Zug. |
|||
===Torsion=== |
|||
[[Bild:Torsion.gif|thumb|Impulsströme in den Wänden eines verdrehten Hohlprofils]] |
|||
Drehimpuls, der in seine eigene Bezugsrichtung transportiert wird, führt zu Torsion. Wie bei der Biegung wird auch bei der Torsion der Drehimpulsstrom von Impulsströmen begrenzt. Nur strömt diesmal die Drehimpulskomponente in ihre eigene Bezugsrichtung und die begleitenden Impulsströme fließen quer. Wählt man die Achse des verdrehten Bauteils in y-Richtung, wird y-Drehimpuls durch das verdrehte Bauteil transportiert. Der Drehimpulsstrom wird dann in x-Richtung von einem x- und in z-Richtung von einem z-Impulsstrom begrenzt. Nach dem Gesetz der zugeordneten Schubspannungen umhüllt ein zusätzlicher Wirbelstrom der y-Komponente den Drehimpulsstrom. Dieser Wirbelstrom ist unter dem Namen Schubfluss bekannt. |
|||
Mathematisch hängt die Stromdichte des y-Impulswirbelstromes in der x-z-Ebene mit dem Drehimpulsstrom gemäss einer einfachen Gradientenregel zusammen. Diese Gradientenregel erlaubt wiederum eine bildhafte Interpretation. Die Stromlinien des Impulswirbelstromes verhalten sich zur Drehimpulsstromstärke wie die Höhenlinien zum Volumen eines Berges. |
|||
===Quellen und Senken=== |
|||
[[Bild:Ströme in Bügel.gif|thumb|Primärer Impulsstrom, Drehimpulsstrom und sekundärer Impulsstrom in einem offenen Bügel]] |
|||
Im belasteten Hebel fließen Impulsströme quer zur Definitionsrichtung. Nach dem Gesetz der zugeordneten Schubspannung erzwingt der in ''x''-Richtung fließende ''z''-Impulsstrom auf seinem ganzen Weg einen in ''z''-Richtung strömenden Impulsstrom der ''x''-Komponente. Damit sind die sich bildenden Wirbel des ''x''-Impulsstromes eigentlich schon erklärt. Die Stromdarstellung kann dennoch um einen zusätzlichen Aspekt erweitert werden. In Anlehnung an die Gravitation darf postuliert werden, dass jeder quer fließende Impulsstrom Quellen oder Senken von Drehimpuls erzeugt. Die Quellenstärke eines Balkenabschnitts folgt aus dem Hebelgesetz. |
|||
Das Zustandekommen der Impulsströme im offenen Bügel kann nun in drei Stufen erklärt werden. Der durch den Bügel fließende ''z''-Impulsstrom repräsentiert den Kraftfluss gemäß der eingangs zitierten Definition. In den Armen des Bügels erzeugt der seitwärts fließende Primärstrom Quellen und Senken, aus denen ''y''-Drehimpulses in das Bauteil hinein- oder aus diesem wegströmt. Im Bauteil selber muss der y-Drehimpulsstrom aus den Quellen die Senken speisen. Die Stärke dieses Drehimpulstransportes ist unter dem Namen Biegemomentenverlauf bekannt. Solange der Drehimpuls in ''x''-Richtung fließt, wird er von Impulsströmen der ''x''-Komponenten begrenzt. Im mittleren Teil des Bügels ist der Drehimpulsstrom von einem ''z''-Impulsstrom berandet. |
|||
[[Bild:Ströme in Bügel2.gif|thumb|Primärer Impulsstrom, Drehimpulsstrom und sekundärer Impulsstrom in einem geschlossenen Bügel]] |
|||
Ersetzt man den offenen Bügel durch einen geschlossenen Rahmen, bilden sich nur in den quer zum „Kraftfluss“ verlaufenden Stücken Drehimpulsströme aus. Dementsprechend verschwindet der Drehimpulstransport samt begleitenden Impulsströmen in den längs ausgerichteten Teilen des Bügels. |
|||
Vergleicht man die Folgerungen, die hier aus der schon lange bekannten Theorie des mechanischen Kontinuums gezogen werden, mit den Eingangs erwähnten Umschreibung des Begriffs Kraftfluss, wird klar, dass mit Kraftfluss entweder der primäre Impulsstrom oder der Strom einer Drehimpulskomponente gemeint ist. Weil die weiteren Implikationen, die sich aus der Symmetrie des Spannungstensors und aus der Verknüpfung der Dreh- und Impulsströme ergeben, nicht berücksichtigt werden, müssen die gängigen "Theorien" bezüglich des Kraftfluss der Metaphysik zugeordnet werden. |
|||
===Platten=== |
|||
Die Gravitation bildet in jedem Bauwerk Impulsquellen aus. Der von diesen Quellen horizontal weg fließende Impuls erzeugt seinerseits Quellen und Senken für den Drehimpuls. Der von den Quellen zu den Senken transportierte Drehimpuls belastet die Bauteile auf Biegung und Torsion. Diese dreistufige Argumentation ist, wenn man sich einmal daran gewöhnt hat, recht anschaulich und funktioniert für Stabwerke und Balken. Wie steht es bei den Platten? Liefern die Impuls- und Drehimpulsbilder bei horizontal ausgerichteten Platten auch eine neue Interpretation für schon bekannte Zusammenhänge? |
|||
In horizontal ausgerichteten Platten kann der z-Impuls sowohl in x- als auch in y-Richtung an die Ränder abfließen. Dementsprechend bilden sich Quellen und Senken sowohl für den y- als auch den x-Drehimpuls. Die zugehörigen Drehimpulsströme bilden Kreise oder, falls die Platte eingespannt ist und nicht nur aufliegt, gehen an die Umgebung weg. Im zweiten Fall heissen die Stärken der wegfliessenden Drehimpulsströme Drehmomente auf die Platten. |
|||
==Statik== |
==Statik== |
||
==Links== |
|||
*[https://www.youtube.com/watch?v=jbHrkhWZcFs Vortrag zu Impulsströmen] |
|||
*[https://cast.switch.ch/vod/clips/2444qq5i3o/link_box Vortrag zu Drehimpulsströmen] |
|||
*[http://www.zhaw.ch/~maur/Lehre/Wiki/Quellekonzept/quelle.html Animation] zu Galgen und Türklinke |
|||
*[http://www.youtube.com/watch?v=EcIqxaidkBQ Impulsstrom] |
|||
*[http://www.youtube.com/watch?v=l5dHIATEGrU Impulsströme in der Statik] |
|||
*[http://www.youtube.com/watch?v=Et2SfAnTadc Kraftfluss] |
|||
*[http://www.youtube.com/watch?v=mVWuVVGE2ss Biegung] |
|||
*[http://www.youtube.com/watch?v=iKcrSgeA_Fk Torsion] |
|||
[[Kategorie:Trans]] [[Kategorie:Rot]] |
|||
Aktuelle Version vom 12. Juni 2014, 14:19 Uhr
Begriff
"Unter dem Kraftfluss versteht man den Weg einer Kraft und/oder eines Moments in einem Bauteil vom Angriffspunkt (Stelle der Einleitung!) bis zur Stelle, an der diese durch eine Reaktionskraft und/oder ein Reaktionsmoment aufgenommen werden" (Quelle: Vorlesungsunterlagen 2002, Prof. Dr.-Ing. Dr. h. c. mult. Uwe Heisel, Institut für Werkzeugmaschinen, Uni Stuttgart)
"Bei der Erarbeitung massstäblicher Entwürfe stellt sich dem Konstrukteur vielfach die Aufgabe, für eine optimale Leitung von Kräften, Drehmomenten und/oder Biegemomenten durch die vorgesehenen Funktionsträger sorgen zu müssen. Zur Veranschaulichung der Funktion Leiten von Kräften und Momenten wird gern der Begriff Kraftfluss verwendet." (Quelle: Hintzen H., Laufenberg H.:Konstruieren und Berechnen, Vieweg)
"Kraftfluss, Kraftleitung: äussere Lasten bewirken Schnittgrössen, die Beanspruchungen (Kräfte, Momente) hervorrufen, welche eleastische oder plastische Verformung hervorrufen." (Quelle: Vorlesungsunterlagen SS 2004 Prof. Dr. Ing. Lucienne Biessing)
Theoretische Grundlagen
In der Punktmechanik kennt man nur Körper und Kräfte, welche zwischen den Körpern wechselwirken. Der Begriff der Kraftleitung ist erst in der technischen Mechanik aufgetaucht, als man mit Hilfe des Schnittprinzips die Konzepte der Newtonschen Punktmechanik und der Eulerschen Starrkörpermechanik auf ausgedehnte Systeme mit einer inneren Struktur übertragen hat.
Zur Beschreibung der Mechanik benötigt man neben der Energie sechs mengenartige oder bilanzierfähige Grössen, die drei Komponenten des Impulses und des Drehimpulses (Nöthersches Theorem). Treten diese sechs Grössen über die materielle Oberfläche eines Körpers, nennt man die zugehörigen Stromstärken Kraft oder Drehmoment. Die drei Kraftkomponenten transformieren sich wie ein Vektor, die drei Komponenten des Drehmomentes wie die drei unabhängigen Komponenten eines schiefsymmetrischen Tensors. Solange man nur eigentliche Transformationen untersucht, verhält sich auch das Drehmoment wie ein Vektor.
Die Stromdichte einer vektorwertige Grösse ist ein Tensor zweiter Stufe; die Stromdichte eines Tensors zweiter Stufe muss mit einem Tensor dritter Stufe beschrieben werden. Nun ist die Stromdichte des Impulses bis auf das Vorzeichen und eine wirkungslose Transposition gleich dem Spannungstensor. Die Stromdichte des Drehimpulsstromes müsste ein spezieller Tensor dritter Stufe sein. Weil in der klassischen Mechanik nur der Impuls lokalisierbar ist, kann für den Drehimpuls aber keine Stromdichte angegeben werden.
Alle in der Literatur gegebenen Definitionen zum Kraftluss sind inkonsistent, weil sie davon ausgehen, dass die vektorwertigen Schnittgrössen Kraft und Drehmoment quasi wie ein Fluss durch die statische Struktur transportiert werden. Nun kann aber nur der Transport einer skalaren Grösse wie Volumen, Masse oder Ladung durch ein einziges Flussbild dargestellt werden.
Impulsstrom
induzierte Wirbelströme
Impuls wird konvektiv und leitungsartig durch den Raum transportiert. Der konvektive Transport, der nur bei Flüssigkeiten und Gasen auftritt, soll hier nicht weiter thematisiert werden. Zur Darstellung des leitungsartigen Impulsstromes nimmt man die Spalten des Spannungstensors, multipliziert diese mit minus eins und zeichnet sie als je einen Pfeil in drei verschiedene Bilder ein. Impulsstrombilder lassen sich problemlos mit Femlab erzeugen. Zu beachten ist, dass die konkrete Gestalt der drei Strombilder von der Wahl des Koordinatensystems abhängt.
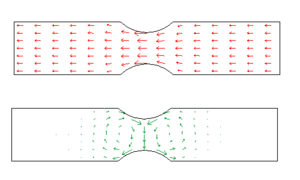
Das erste Bild zeigt den Impulsstrom durch einen beidseits eingekerbten Blechstreifen. Im Bereich der Kerben wird der primäre Impulsstrom gegen die Mitte hin abgelenkt. Dabei entstehen Wirbelströme der zweiten Impulskomponente. Schuld an dieser Wirbelbildung ist das Prinzip der zugeordneten Schubspannung (Symmetrie des Spannungstensors). In der Sprache der Impulsströme besagt dieses Prinzip, dass ein y-Impulsstrom in x-Richtung fließen muss, sobald der x-Impulsstrom in die y-Richtung ausweicht. Allgemein formuliert muss die j-Komponente der i-Impulsstromdichte an jedem Ort gleich der i-Komponente der j-Impulsstromdichte sein (i und j stehen für x, y und z).
Prinzip der direkten Kraftleitung
Das Prinzip der direkten Kraftleitung besagt, dass die Kraft in ihre eigene Wirkrichtung „abgeleitet“ werden soll. Übersetzt man diese Aussage ins Impulsstrombild, bedeutet dies, dass jede Impulskomponente möglichst in ihre eigene Richtung strömen soll. Andernfalls werden Wirbelströme induziert. Diese Übersetzung vom Kraft- ins Impulsstrombild trifft jedoch nur zu, wenn eine Achse des globalen Koordinatensystems mit der Kraftrichtung zusammenfällt. Nur dann fließt bei reiner Zug- oder Druckbelastung eine einzige Impulskomponente in ihre eigene Bezugsrichtung. Bei allgemeiner Ausrichtung fließen zwei oder sogar drei Impulskomponenten gleichzeitig durch das unter Zug- oder Druck stehende Bauteil. Das Dilemma zwischen nur global gültigem Strombild und lokaler Analyse bezüglich der Hauptspannungsrichtung lässt sich durch Einführung von bauteilspezifischen Koordinatensystemen lösen. Im einfachsten Fall der Zug- und Druckstäbe reduziert sich das lokale Koordinatensystem auf einen Bezugspfeil. Wie man damit umgeht, kann anhand einfacher Fachwerk gezeigt werden.
Prinzip der kurzen Kraftleitung
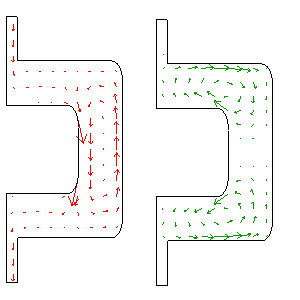
Der Kraftfluss soll direkt und kurz geführt sein. Direkt und kurz geführte Kraftflüsse verursachen keine unnötigen Wirbel. Muss der in einem Zugstab in seine eigene Bezugsrichtung fließende Impulsstrom aus konstruktiven Gründen umgeleitet werden, induziert er gemäß dem Prinzip der zugeordneten Schubspannung einen zusätzlichen Strom. Im Kopplungsgebiet fließen Primär- und Sekundärstrom mit der gleichen Stromdichte in die Richtung der jeweils andern Komponenten. Weil der Sekundärstrom nicht durch die Oberfläche des Bauteils treten kann, schließt er sich im Innern des Bauteils zu einem Kreis.
Die Wirbelbildung soll nun anhand eines einfachen Beispiels diskutiert werden. Ersetzt man einen Teil eines Zugstabes durch einen offenen Bügel, muss der primäre Impulsstrom in den Armen des Bügels seitwärts zu seiner Bezugsrichtung fließen. Dabei induziert er gemäß dem Gesetz der zugeordneten Schubspannungen zwei Sekundärströme, die sich über den beiden Armen des Bügels zu je einem Wirbel schließen. In beiden Ecken des Bügels fließen die Sekundärströme seitwärts und induzieren dabei einen Tertiärstrom, der sich über den mittleren Teil des Bügels zu einem Wirbel schließt. Primär- und Tertiärstrom transportieren die gleiche Impulskomponente und bilden zusammen einen Gesamtstrom (linkes Teilbild). Im rechten Teilbild kann man die zwei Wirbelströme der Sekundärkomponente deutlich erkennen.
Prinzip des Kraftausgleichs
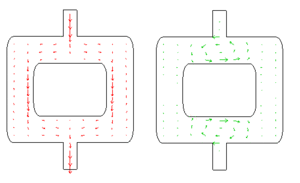
Ersetzt man den offenen Bügel durch einen geschlossenen, spaltet sich der primäre Impulsstrom in zwei Teile auf. Der seitwärts fließende Primärstrom induziert Sekundärströme, die sich über den beiden Doppelarmen zu je einem Wirbel schließen. Dank dieser Symmetrie baut sich nur ein schwacher Tertiärstrom auf.
Hinter dem Prinzip des Kraftausgleichs steht eine gewisse Ökonomie in Bezug auf die Ausbildung von Sekundärwirbel. In jedem Wirbel fließt der Impuls ein Stück weit in seine eigene Bezugsrichtung, was sich als Druck bemerkbar macht. Auf der gegenüberliegenden Seite fließt der Impuls unter Zugbelastung gegen die Bezugsrichtung. Dazwischen muss der Impuls seitwärts transportiert werden und folglich mit dem Strom einer zweiten Impulskomponente koppeln. Das Prinzip des Kraftausgleichs sorgt nun dafür, dass der Primärstrom beide Seiten des Sekundärwirbels abdeckt. Dann gibt es keine freie Flanke mehr, auf der ein Tertiärwirbel aufgebaut werden kann.
Impulsquellen
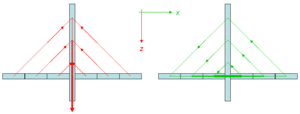
In der Statik bilden Impulsströme über mehrere Bauteile Kreise und in den einzelnen Bauteilen Wirbel aus. Nur die Gravitationskraft vermag diese Kreisströme aufzubrechen. Die Gravitationskraft steht für den volumenmäßigen Impulsaustausch zwischen Körper und Gravitationsfeld. Zeigt die positive z-Achse nach unten, besitzt jeder Körper eine z-Impulsquelle. Diese Quelle verteilt sich über das ganze Volumen. Die Quellendichte ist gleich Massendichte mal Gravitationsfeldstärke. Das Bild zeigt die Impulsströme in einer Schrägseilbrücke. Der z-Impuls, der vom Gravitationsfeld her zuströmt, wird über die Seile schief nach oben an die Pylone abgeführt. In den schief stehenden Seilen strömt zusätzlich noch Impuls der x-Komponente.
In der Dynamik muss das Impulsspeichervermögen der einzelnen Körper konsistent mit den zugehörigen Strömen, den Kräften, verknüpft werden. Weil sich die träge Masse nicht von der schweren Masse unterscheidet, erzeugen beschleunigte Körper die gleichen Impulsströme wie ruhende Körper im entsprechenden Gravitationsfeld. Ein Impulsstrom kann also sowohl von einer Änderungsrate des Impulsinhaltes als auch von einem Gravitationsfeld gespiesen werden. Diese doppelte Wirkung der Masse, einmal als Impulskapazität und einmal als Teil der Quellenstärke, schafft große Verständnisprobleme in Bezug auf den Kraftbegriff. Erschwerend kommt hinzu, dass in der technischen Mechanik der Bergriff der Trägheitskraft nach d’Alambert dazu benutzt wird, ein dynamisches Problem auf ein statisches zurückzuführen, in der Physik Trägheitskräfte aber nur dann eingeführt werden, wenn das Beobachtersystem im Sinne von Newton und Mach nichtinertial ist.
Drehimpulsstrom
Der Drehimpuls darf wie jede andere mengenartige Größe bezüglich eines Systems bilanziert werden. Nur sind beim Drehimpuls weder Inhalt noch Stromstärke direkt messbar. Dass diese Einschränkung den Wert des Bilanzierens nicht zu schmälern vermag, zeigt sich schon bei der Energie. Viele Fragestellungen der Mechanik lassen sich mit Hilfe der Energie lösen, obwohl weder der Energietransport noch der Energieinhalt direkt gemessen werden können. Wenn nachfolgend von Drehimpulsinhalt oder Drehimpulsstrom die Rede ist, wird nicht behauptet, dass diese Größe in jedem Fall lokalisierbar sei. Zudem hängt der konkrete Wert des Drehimpulsinhalts oder des Drehimpulsstromes von der Wahl des Koordinatensystems ab.
Bedingte Lokalisierbarkeit
Üblicherweise schreibt man einer Punktmasse einen Drehimpuls bezüglich eines raumfesten Referenzpunktes zu. Entsprechend verfährt man mit dem Drehmoment. Der Drehimpuls ist so gesehen eine nichtlokale Erhaltungsgröße, deren absoluter Wert von der Lage des Bezugspunktes abhängt. Erst mit der Physik des 20. Jahrhunderts hat sich der Eigendrehimpuls unter dem Namen Spin zu einer Größe gewandelt, die wie die elektrische Ladung oder die Masse direkt einem System zugeschrieben wird.
Die bedingte Lokalisierbarkeit ist einer der Gründe, weshalb der Drehimpuls kaum als bilanzierfähige Größe wahrgenommen wird. Für den Drehimpuls kann weder eine direkt messbare Dichte noch eine lokal nachweisbare Stromdichte definiert werden. Die Bilanzgleichung leitet sich folglich nicht wie bei der elektrischen Ladung oder beim Impuls aus der Kontinuitätsgleichung ab.
Drehimpulsströme
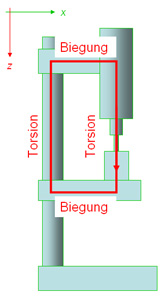
Ein raumfestes Koordinatensystem zerlegt den Drehimpuls in seine drei Komponenten. Jede der drei Drehimpulskomponenten kann in die eigene Bezugsrichtung oder seitwärts dazu transportiert werden. Drehimpulsströme sind aber nur mittelbar, über die sie begleitenden Impulsströme nachweisbar. Fließt der Drehimpuls in seine eigene Bezugsrichtung durch ein Bauteil, liegt Torsion vor. Bei einem Transport seitwärts zu Bezugsrichtung erleidet das Bauteil Biegung. Biegung und Torsion sind somit direkte Auswirkungen eines Drehimpulstransports.
Diese einfache Zuordnung zwischen Drehimpulstransport und Bauteilreaktion kommt der Idee eines makroskopischen Kraftflusses schon ziemlich nahe. Betrachten wir dazu eine Ständerbohrmaschine. Der z-Drehimpuls, der im Bohrer vorwärts fließt, bildet über Tisch, Säule, Halterung, Motor und Spindel einen Kreisstrom. In der Säule, in der Spindel und im Bohrer erzeugt der Drehimpulsstrom Torsion, in den Halterungen für Tisch und Motor herrscht Biegung. In diesem Beispiel ist der „Kraftfluss“ ein Drehimpulsstrom, dessen Stärke je nach Transportrichtung als Torsions- oder Biegemoment bezüglich einer Schnittebene bestens bekannt ist.
Die bildhafte Darstellung des Drehimpulses reicht weit über die Konkretisierung des Kraftflusses hinaus. Eine mit Hilfe des Drehimpulses entwickelte Rotationsmechanik lässt sich problemlos in die allgemeine Systemtheorie einbetten. Mit der Winkelgeschwindigkeit als Potenzialgröße kann jedem Drehimpulsstrom ein Energiestrom zugeordnet werden. Torsionsfedern werden so zu Induktivitäten, Massenträgheitsmomente zu Kapazitäten und Reibflächen zu (nichtlinearen) Widerständen. In der Ständerbohrmaschine wird der Drehimpulsstrom im Elektromotor mit Energie beladen. Diese Energie setzt der Drehimpulsstrom zwischen Schnittfläche und Span wieder frei.
Biegung
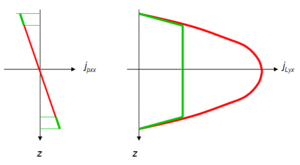
Bei Biegung wird der im Balken seitwärts fließende Drehimpulsstrom beidseits von einem Impulsstrom begrenzt. Die Impulsstromdichte ist gleich dem Gradienten der Drehimpulsstromdichte normal zur Transport- und normal zur Bezugsrichtung der Drehimpulskomponente. Die Skizze zeigt das Impuls- und Drehimpulsstromdichteprofil quer zum gebogenen Balken. Die rote Linien beziehen sich auf die Verhältnisse im Steg, die grünen Linien beschreiben die Stromdichten längs einer Linie, welche nur die Gurten normal durchstösst. Die konkrete Gestalt der Impulsstromdichte, die Verteilung der Zug- und Druckspannungen, hängt von den Materialeigenschaften ab. Die Drehimpulsstromdichte ist dann aber nur noch von der Impulsstromdichte abhängig.
Bei der reinen Biegung wird Drehimpuls seitwärts zur Definitionsrichtung transportiert. Der Drehimpulstransport wird beidseits von einem Impulsstrom begrenzt, wobei die Impulsstromdichte gleich der Änderung der Drehimpulsstromdichte normal zu den Definitionsrichtungen von Impuls und Drehimpuls ist. Weil der Impuls in oder gegen seine eigene Bezugsrichtung fließt, erzeugt er Druck oder Zug.
Torsion
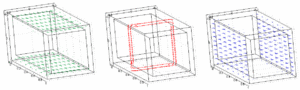
Drehimpuls, der in seine eigene Bezugsrichtung transportiert wird, führt zu Torsion. Wie bei der Biegung wird auch bei der Torsion der Drehimpulsstrom von Impulsströmen begrenzt. Nur strömt diesmal die Drehimpulskomponente in ihre eigene Bezugsrichtung und die begleitenden Impulsströme fließen quer. Wählt man die Achse des verdrehten Bauteils in y-Richtung, wird y-Drehimpuls durch das verdrehte Bauteil transportiert. Der Drehimpulsstrom wird dann in x-Richtung von einem x- und in z-Richtung von einem z-Impulsstrom begrenzt. Nach dem Gesetz der zugeordneten Schubspannungen umhüllt ein zusätzlicher Wirbelstrom der y-Komponente den Drehimpulsstrom. Dieser Wirbelstrom ist unter dem Namen Schubfluss bekannt.
Mathematisch hängt die Stromdichte des y-Impulswirbelstromes in der x-z-Ebene mit dem Drehimpulsstrom gemäss einer einfachen Gradientenregel zusammen. Diese Gradientenregel erlaubt wiederum eine bildhafte Interpretation. Die Stromlinien des Impulswirbelstromes verhalten sich zur Drehimpulsstromstärke wie die Höhenlinien zum Volumen eines Berges.
Quellen und Senken
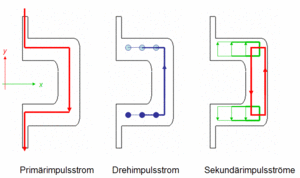
Im belasteten Hebel fließen Impulsströme quer zur Definitionsrichtung. Nach dem Gesetz der zugeordneten Schubspannung erzwingt der in x-Richtung fließende z-Impulsstrom auf seinem ganzen Weg einen in z-Richtung strömenden Impulsstrom der x-Komponente. Damit sind die sich bildenden Wirbel des x-Impulsstromes eigentlich schon erklärt. Die Stromdarstellung kann dennoch um einen zusätzlichen Aspekt erweitert werden. In Anlehnung an die Gravitation darf postuliert werden, dass jeder quer fließende Impulsstrom Quellen oder Senken von Drehimpuls erzeugt. Die Quellenstärke eines Balkenabschnitts folgt aus dem Hebelgesetz.
Das Zustandekommen der Impulsströme im offenen Bügel kann nun in drei Stufen erklärt werden. Der durch den Bügel fließende z-Impulsstrom repräsentiert den Kraftfluss gemäß der eingangs zitierten Definition. In den Armen des Bügels erzeugt der seitwärts fließende Primärstrom Quellen und Senken, aus denen y-Drehimpulses in das Bauteil hinein- oder aus diesem wegströmt. Im Bauteil selber muss der y-Drehimpulsstrom aus den Quellen die Senken speisen. Die Stärke dieses Drehimpulstransportes ist unter dem Namen Biegemomentenverlauf bekannt. Solange der Drehimpuls in x-Richtung fließt, wird er von Impulsströmen der x-Komponenten begrenzt. Im mittleren Teil des Bügels ist der Drehimpulsstrom von einem z-Impulsstrom berandet.
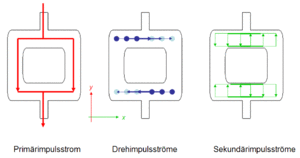
Ersetzt man den offenen Bügel durch einen geschlossenen Rahmen, bilden sich nur in den quer zum „Kraftfluss“ verlaufenden Stücken Drehimpulsströme aus. Dementsprechend verschwindet der Drehimpulstransport samt begleitenden Impulsströmen in den längs ausgerichteten Teilen des Bügels.
Vergleicht man die Folgerungen, die hier aus der schon lange bekannten Theorie des mechanischen Kontinuums gezogen werden, mit den Eingangs erwähnten Umschreibung des Begriffs Kraftfluss, wird klar, dass mit Kraftfluss entweder der primäre Impulsstrom oder der Strom einer Drehimpulskomponente gemeint ist. Weil die weiteren Implikationen, die sich aus der Symmetrie des Spannungstensors und aus der Verknüpfung der Dreh- und Impulsströme ergeben, nicht berücksichtigt werden, müssen die gängigen "Theorien" bezüglich des Kraftfluss der Metaphysik zugeordnet werden.
Platten
Die Gravitation bildet in jedem Bauwerk Impulsquellen aus. Der von diesen Quellen horizontal weg fließende Impuls erzeugt seinerseits Quellen und Senken für den Drehimpuls. Der von den Quellen zu den Senken transportierte Drehimpuls belastet die Bauteile auf Biegung und Torsion. Diese dreistufige Argumentation ist, wenn man sich einmal daran gewöhnt hat, recht anschaulich und funktioniert für Stabwerke und Balken. Wie steht es bei den Platten? Liefern die Impuls- und Drehimpulsbilder bei horizontal ausgerichteten Platten auch eine neue Interpretation für schon bekannte Zusammenhänge?
In horizontal ausgerichteten Platten kann der z-Impuls sowohl in x- als auch in y-Richtung an die Ränder abfließen. Dementsprechend bilden sich Quellen und Senken sowohl für den y- als auch den x-Drehimpuls. Die zugehörigen Drehimpulsströme bilden Kreise oder, falls die Platte eingespannt ist und nicht nur aufliegt, gehen an die Umgebung weg. Im zweiten Fall heissen die Stärken der wegfliessenden Drehimpulsströme Drehmomente auf die Platten.
Statik
Links
- Vortrag zu Impulsströmen
- Vortrag zu Drehimpulsströmen
- Animation zu Galgen und Türklinke
- Impulsstrom
- Impulsströme in der Statik
- Kraftfluss
- Biegung
- Torsion