Lösung zu Volumen bilanzieren: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 27. September 2010, 13:59 Uhr

Lösungsidee

Bei linearer Änderung der Stromstärke darf mit dem zeitlichen Mittelwert gearbeitet werden.
Die Volumenänderung über einem Zeitabschnitt kann auf zwei Arten berechnet werden:
- entweder summiert (integriert) man die einzelnen Stromstärken über die Zeit und zählt dann alles zusammen
- oder man bestimmt zuerst die Änderungsrate und summiert (integriert) dann über die Zeit.

Volumenströme: Prinzip und Diagramm

Lösung

Als Volumenänderungsrate resultiert:

[math]\dot V=I_{V_1}-I_{V_2}-I_{V_3}[/math]

Am Anfang (t = 0 s) ist diese: 3 dl/s - 6 dl/s - 12 dl/s = -15 dl/s

Am Schluss (t = 180 s): 9 dl/s - 6 dl/s - 3 dl/s = 0 dl/s

Die in den Strömen geflossenen (gf) Volumina werden als Fläche unter den 3 Kurven (Dreiecke) berechnet und ergeben die Volumenänderung des Systems:

[math]\Delta V=V_{gf_1}-V_{gf_2}-V_{gf_3}[/math]= (6 dl/s - 6 dl/s - 7.5 dl/s) * 180 s = -1350 dl = -135 l

Alternativ dazu kann die Volumenänderungs des Gerätes auch aus der Volumenänderungsrate berechnet werden, ebenfalls als Fläche unter der Kurve. Das ergibt ebenfalls: 1/2 * 180 s * (-1.5 l/s) = -135 l.

Aufgabe

@@ Zeile 1: / Zeile 1: @@
 ==Lösungsidee==
-Bei linearer Änderung der Stromstärke darf mit dem zeitlichen Mittelwert gearbeitet werden. Die Volumenänderung über einem Zeitabschnitt kann auf zwei Arten berechnet werden: entweder integriert man über die einzelnen Stromstärken auf und zählt dann alles zusammen oder man bestimmt das Zeitintegral direkt über der [[Änderungsrate]].
+*Bei linearer Änderung der Stromstärke darf mit dem zeitlichen Mittelwert gearbeitet werden.
+*Die Volumenänderung über einem Zeitabschnitt kann auf zwei Arten berechnet werden:
+**entweder summiert (integriert) man die einzelnen Stromstärken über die Zeit und zählt dann alles zusammen
+**oder man bestimmt zuerst die [[Änderungsrate]] und summiert (integriert) dann über die Zeit.
+[[Bild:Volumen_bilanzieren.png]]
-Wenn sich sowohl der Druck als auch Volumenstromstärke linear mit der Zeit ändern, ist die Prozessleistung eine quadratische Funktion in der Zeit. Wer die Integralrechnung noch nicht beherrscht, muss die Lösung graphisch suchen (Fläche unter der [[Energiestrom-Zeit-Diagramm]] oder Volumen im  [[Strom-Potenzial-Zeit-Schaubild]]) .
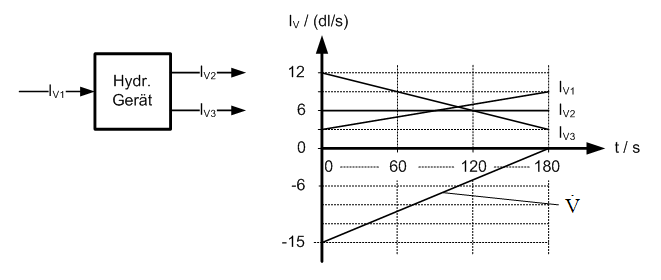
+Volumenströme: Prinzip und Diagramm
 ==Lösung==
+Als Volumenänderungsrate resultiert:
-<math>\sum_{i} I_{Vi} = \dot V</math>
+:<math>\dot V=I_{V_1}-I_{V_2}-I_{V_3}</math>
-Am Anfang: 3 dl/s - 6 dl/s - 12 dl/s = -15 dl/s
-Am Schluss: 9 dl/s - 6 dl/s - 3 dl/s = 0 dl/s
+Am Anfang (t = 0 s) ist diese: 3 dl/s - 6 dl/s - 12 dl/s = -15 dl/s
+Am Schluss (t = 180 s): 9 dl/s - 6 dl/s - 3 dl/s = 0 dl/s
-<math>\sum_{i} V_{ausi} = \Delta V</math>
+Die in den Strömen geflossenen (gf) Volumina werden als Fläche unter den 3 Kurven (Dreiecke) berechnet und ergeben die Volumenänderung des Systems:
-(0.6 l/s - 0.6 l/s - 0.75 l/s)180 s = -135 l
+:<math>\Delta V=V_{gf_1}-V_{gf_2}-V_{gf_3}</math>= (6 dl/s - 6 dl/s - 7.5 dl/s) * 180 s = -1350 dl = -135 l
+Alternativ dazu kann die Volumenänderungs des Gerätes auch aus der Volumenänderungsrate berechnet werden, ebenfalls als Fläche unter der Kurve. Das ergibt ebenfalls:
-Über die Zuleitung fliesst ein [[zugeordneter Energiestrom]], der sich quadratisch in der Zeit ändert. Die integration über die Zeit, die Fläche unter dem [[Energiestrom-Zeit-Diagramm]] oder das Volumen im [[Strom-Potenzial-Zeit-Schaubild]] liefert 729 kJ.
+/2 * 180 s * (-1.5 l/s) = -135 l.
-<br>'''[[Volumen bilanzieren|Aufgabenstellung]]'''
+'''[[Volumen bilanzieren|Aufgabe]]'''