Kondensator entladen: Unterschied zwischen den Versionen
User (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
Die Ladungsbilanz bezüglich des einen Teils des Kondensators bildet den Ausgangspunkt unserer Überlegungen |
Die Ladungsbilanz bezüglich des einen Teils des Kondensators bildet den Ausgangspunkt unserer Überlegungen |
||
<math>\dot Q = I</math> |
:<math>\dot Q = I</math> |
||
Ersetzt man nun die Änderungsrate der Ladung mit Hilfe des [[kapazitives Gesetz|kapazitiven]] und den Strom über das [[resistives Gesetz|resistive Gesezt]], erhält man die Differentialgleichung für dieses Problem |
Ersetzt man nun die Änderungsrate der Ladung mit Hilfe des [[kapazitives Gesetz|kapazitiven]] und den Strom über das [[resistives Gesetz|resistive Gesezt]], erhält man die Differentialgleichung für dieses Problem |
||
<math>C \dot U = -\frac {U}{R}</math> oder <math>RC \dot U + U = 0</math> |
:<math>C \dot U = -\frac {U}{R}</math> oder <math>RC \dot U + U = 0</math> |
||
Das Minuszeichen hängt mit den unterschiedlichen Betrachtungsweisen zusammen: Die Ladungsbilanz wird bezüglich des Kondensators aufgestellt, das resistive Gesetz bezieht sich auf den Widerstand. |
Das Minuszeichen hängt mit den unterschiedlichen Betrachtungsweisen zusammen: Die Ladungsbilanz wird bezüglich des Kondensators aufgestellt, das resistive Gesetz bezieht sich auf den Widerstand. |
||
| Zeile 17: | Zeile 17: | ||
Die Differentialgleichung besagt, dass die Spannung zur (negativen) Änderungsrate der Spannung proportional ist. Folglich ist besteht die Lösung dieser Gleichung in einer (abklingenden) Exponentialfunktion |
Die Differentialgleichung besagt, dass die Spannung zur (negativen) Änderungsrate der Spannung proportional ist. Folglich ist besteht die Lösung dieser Gleichung in einer (abklingenden) Exponentialfunktion |
||
<math>U = U_0 e^{-t / \tau}</math> mit ''τ = RC'' |
:<math>U = U_0 e^{-t / \tau}</math> mit ''τ = RC'' |
||
Die exponentielle Abnahme der Spannung über dem Widerstand zieht eine entsprechende Abnahme der Stromstärke nach sich |
Die exponentielle Abnahme der Spannung über dem Widerstand zieht eine entsprechende Abnahme der Stromstärke nach sich |
||
<math>I = I_0 e^{-t / \tau}</math> mit ''I<sub>0</sub>'' = ''U<sub>0</sub>/R'' |
:<math>I = I_0 e^{-t / \tau}</math> mit ''I<sub>0</sub>'' = ''U<sub>0</sub>/R'' |
||
Entsprechend sinkt auch die Leistung über dem Widerstand |
Entsprechend sinkt auch die Leistung über dem Widerstand |
||
<math>P = P_0 e^{-2t / \tau}</math> mit ''P<sub>0</sub>'' = ''U<sub>0</sub> I<sub>0</sub>'' = ''U<sub>0</sub><sup>2</sup> / R'' = ''R I<sub>0</sub><sup>2</sup>'' |
:<math>P = P_0 e^{-2t / \tau}</math> mit ''P<sub>0</sub>'' = ''U<sub>0</sub> I<sub>0</sub>'' = ''U<sub>0</sub><sup>2</sup> / R'' = ''R I<sub>0</sub><sup>2</sup>'' |
||
==Systemdynamik== |
==Systemdynamik== |
||
| Zeile 34: | Zeile 34: | ||
==Simulation== |
==Simulation== |
||
| ⚫ | [[Bild:Kondensator_entladen_D1.png|thumb|Systemdiagramm einer Kondensatorentladung]] Strom und Spannung nehmen exponentiell mit der Zeit ab. Würde die Stromstärke nicht abnehmen, wäre der Kondensator nach der Zeit '''''τ = RC''''' entladen. Im wirklichen System und auch in der Simulation sinken Strom und Spannung nach dieser Zeit auf den ''e''-ten Teil des Anfangswert ab. Diese Überlegung kann fortgesetzt werden. Nach jeder Zeitkonstante vermindert sich die Spannung auf den ''e''-ten Teil des entsprechenden Anfangswertes. |
||
[[Bild:Kondensator_entladen_D1.png|thumb|Systemdiagramm einer Kondensatorentladung]] |
|||
| ⚫ | |||
==analytische Lösung== |
|||
Dieses Problem kann recht einfach analytisch gelöst werden. Für die Spannung erhält man dann eine sinkende Exponentialfunktion bezüglich der Zeit |
|||
:<math>U = U_a e^{-t/\tau}</math> |
|||
Indem man das Ohm'sche Gesetz auf den Widerstand anwendet, erhält man die Strom-Zeit-Funktion |
|||
:<math>I= I_a e^{-t/\tau}</math> mit ''I<sub>a</sub>'' = ''U<sub>a</sub>/R'' |
|||
Die über dem Widerstand dissipierte Leistung ist dann gleich dem Produkt dieser beiden Funktionen |
|||
:<math>P= P_a e^{-2t/\tau}</math> mit ''P<sub>a</sub>'' = ''U<sub>a</sub>I<sub>a</sub>'' = ''U<sub>a</sub><sup>2</sup>/R'' = ''I<sub>a</sub><sup>2</sup>R'' |
|||
[[Kategorie:Elektro]] [[Kategorie: ElektroMod]] |
[[Kategorie:Elektro]] [[Kategorie: ElektroMod]] |
||
Aktuelle Version vom 27. Mai 2008, 12:09 Uhr
Problemstellung
Ein Kondensator wird zuerst auf eine bestimmte Spannung aufgeladen und dann über einem Widerstand wieder entladen. Beim Entladen fliesst die elektrische Ladung von einem Teil des Kondensators zum andern und setzt dabei über dem Widerstand Energie frei.
Dieser Vorgang kann problemlos ins Flüssigkeitsbild übertragen werden. Dazu denkt man sich den einen Teil des Kondensators geerdet. Dann dürfen der andere Teil des Kondensators und der Widerstand mit einem Gefäss verglichen werden, aus dem eine zähe Flüssigkeit über ein langes Röhrchen ausläuft.
Dynamik
Die Ladungsbilanz bezüglich des einen Teils des Kondensators bildet den Ausgangspunkt unserer Überlegungen
- [math]\dot Q = I[/math]
Ersetzt man nun die Änderungsrate der Ladung mit Hilfe des kapazitiven und den Strom über das resistive Gesezt, erhält man die Differentialgleichung für dieses Problem
- [math]C \dot U = -\frac {U}{R}[/math] oder [math]RC \dot U + U = 0[/math]
Das Minuszeichen hängt mit den unterschiedlichen Betrachtungsweisen zusammen: Die Ladungsbilanz wird bezüglich des Kondensators aufgestellt, das resistive Gesetz bezieht sich auf den Widerstand.
Die Differentialgleichung besagt, dass die Spannung zur (negativen) Änderungsrate der Spannung proportional ist. Folglich ist besteht die Lösung dieser Gleichung in einer (abklingenden) Exponentialfunktion
- [math]U = U_0 e^{-t / \tau}[/math] mit τ = RC
Die exponentielle Abnahme der Spannung über dem Widerstand zieht eine entsprechende Abnahme der Stromstärke nach sich
- [math]I = I_0 e^{-t / \tau}[/math] mit I0 = U0/R
Entsprechend sinkt auch die Leistung über dem Widerstand
- [math]P = P_0 e^{-2t / \tau}[/math] mit P0 = U0 I0 = U02 / R = R I02
Systemdynamik
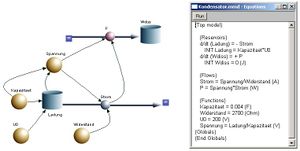
Das Systemdiagramm für das Entladen eines Kondensators über einem Widerstand kann direkt aus dem Flüssigkeitsbild gewonnen werden. Der eine Teil des Kondensators bildet den Topf (Stock), der Stromzweig über dem Widerstand das Abflussrohr (flow).
Die Spannung legt die Ladung auf dem Kondensator sowie die Stromstärke durch den Widerstand fest. Als zweite Ebene ist die Energiebetrachtung mitmodelliert. Integriert man die über dem Widerstand umgesetzte Leistung über die Zeit auf, erhält man die total dissibierte Leistung, die gerade der Kondensatorenergie zu Beginn der Vorganges entspricht (W = C/2 U2). Im Flüssigkeitsbild erscheint die im Kondensator gespeicherte Energie als Lageenerige bezüglich des grossen Sees: Menge mal mittlere Pumphöhe.
Simulation
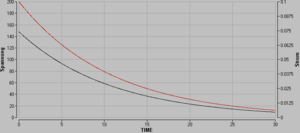
Strom und Spannung nehmen exponentiell mit der Zeit ab. Würde die Stromstärke nicht abnehmen, wäre der Kondensator nach der Zeit τ = RC entladen. Im wirklichen System und auch in der Simulation sinken Strom und Spannung nach dieser Zeit auf den e-ten Teil des Anfangswert ab. Diese Überlegung kann fortgesetzt werden. Nach jeder Zeitkonstante vermindert sich die Spannung auf den e-ten Teil des entsprechenden Anfangswertes.
analytische Lösung
Dieses Problem kann recht einfach analytisch gelöst werden. Für die Spannung erhält man dann eine sinkende Exponentialfunktion bezüglich der Zeit
- [math]U = U_a e^{-t/\tau}[/math]
Indem man das Ohm'sche Gesetz auf den Widerstand anwendet, erhält man die Strom-Zeit-Funktion
- [math]I= I_a e^{-t/\tau}[/math] mit Ia = Ua/R
Die über dem Widerstand dissipierte Leistung ist dann gleich dem Produkt dieser beiden Funktionen
- [math]P= P_a e^{-2t/\tau}[/math] mit Pa = UaIa = Ua2/R = Ia2R