Lösung zu Teilelastischer Stoss: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Bild:TeilelastischerStoss.jpg|thumb|Flüssigkeitsbild]] |
[[Bild:TeilelastischerStoss.jpg|thumb|Flüssigkeitsbild]] |
||
Alle relevanten Informaitonen können direkt dem Flüssigkeitsbild entnommen werden: |
Alle relevanten Informaitonen können direkt dem Flüssigkeitsbild entnommen werden. Man berechnet zuerst die Geschwindigkeiten und ihre Differenzen, siehe Flüssigkeitsbild: |
||
*die inelastische Geschwindigkeit beträgt <math>v_{in} = \frac {0.6 kg \cdot 1.6 m/s + 0.4 kg \cdot -0.4 m/s}{0.6 kg + 0.4 kg}</math> = 0.8 m/s |
*die inelastische Geschwindigkeit beträgt <math>v_{in} = \frac {0.6 kg \cdot 1.6 m/s + 0.4 kg \cdot -0.4 m/s}{0.6 kg + 0.4 kg}</math> = 0.8 m/s |
||
*die Geschwindigkeitsdifferenz des Fahrzeugs von links beträgt in der 1. Phase 1.6 m/s - 0.8 m/s = 0.8 ms und in der 2. Phase 0.8 m/s - 0.1 m/s = 0.7 m/s |
|||
*das Verhältnis zwischen den Geschwindigkeitsänderungen für die beiden Stossphasen ist für beide Wagen gleich <math>\frac {0.8 m/s}{0.7 m/s} = \frac {1.2 m/s}{1.05 m/s}</math> |
|||
*ihr Verhältnis also 0.7 m/s / 0.8 m/s = 0.875 |
|||
*die maximale Fallhöhe beträgt 2 m/s und die Pumphöhe erreicht einen Wert von 1.75 m/s |
|||
*die Geschwindigkeitsdifferenz des Fahrzeugs von rechts beträgt in der 1. Phase 0.8 m/s - (-0.4 m/s) = 1.2 ms |
|||
*das Verhältnis der Geschwindigkeitsdifferenzen in den Stossphasen ist für beide Wagen gleich. Also berechnet man für den Wagen von rechts die Geschwindigkeitsdifferenz der 2. Phase zu 0.875 * 1.2 m/s = 1.05 m/s |
|||
*daraus ergibt sich eine Endgeschwindigkeit des Wagens von rechts von 0.8 m/s + 1.05 m/s = 1.85 m/s |
|||
*die maximale Fallhöhe des Impulses (zu Beginn des Stosses) beträgt 1.6 m/s - (-0.4 m/s) = 2.0 m/s und die max. Pumphöhe (am Ende des Stosses) erreicht einen Wert von 1.85 m/s - 0.1 m/s = 1.75 m/s. Die mittlere Fallhöhe beträgt hier die Hälfte, also 1 m/s, analog die mittlere Pumphöhe 0.875 m/s |
|||
*beim Fallen (1. Stossphase) fliesst ein Impuls von 0.8 m/s * 0.6 kg = 0.48 Ns, beim Pumpen (2. Stossphase) von 0.7 m/s * 0.6 kg = 0.42 Ns |
|||
Damit ist die Aufgabe gelöst: |
Damit ist die Aufgabe gelöst: |
||
#Am Schluss gleitet das leichtere Fahrzeug mit einer Geschwindigkeit von 1.85 m/s nach rechts. |
#Am Schluss gleitet das leichtere Fahrzeug mit einer Geschwindigkeit von 1.85 m/s nach rechts. |
||
#In der ersten Teilphase setzt der Impuls |
#In der ersten Teilphase setzt der Impuls die folgende Energiemenge frei <math>W_{frei} = 0.48 Ns * 1 m/s = 0.48 J</math> (geflossener Impuls mal mittlere Fallhöhe). In der zweiten Teilphase nimmt der Impuls einen Teil dieser Energie wieder zurück <math>W_{auf} = 0.42 Ns * 0.875 m/s = 0.368 J</math>. |
||
Das Verhältnis |
Das Verhältnis der vom Impuls freigesetzten Energie zur vom Impuls wieder aufgenommenen ist gleich dem Quadrat des Verhältnis der zugehörigen Geschwinigkeitsänderungen. |
||
'''[[Teilelastischer Stoss|Aufgabe]]''' |
'''[[Teilelastischer Stoss|Aufgabe]]''' |
||
Aktuelle Version vom 21. November 2013, 20:54 Uhr
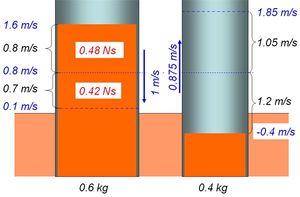
Alle relevanten Informaitonen können direkt dem Flüssigkeitsbild entnommen werden. Man berechnet zuerst die Geschwindigkeiten und ihre Differenzen, siehe Flüssigkeitsbild:
- die inelastische Geschwindigkeit beträgt [math]v_{in} = \frac {0.6 kg \cdot 1.6 m/s + 0.4 kg \cdot -0.4 m/s}{0.6 kg + 0.4 kg}[/math] = 0.8 m/s
- die Geschwindigkeitsdifferenz des Fahrzeugs von links beträgt in der 1. Phase 1.6 m/s - 0.8 m/s = 0.8 ms und in der 2. Phase 0.8 m/s - 0.1 m/s = 0.7 m/s
- ihr Verhältnis also 0.7 m/s / 0.8 m/s = 0.875
- die Geschwindigkeitsdifferenz des Fahrzeugs von rechts beträgt in der 1. Phase 0.8 m/s - (-0.4 m/s) = 1.2 ms
- das Verhältnis der Geschwindigkeitsdifferenzen in den Stossphasen ist für beide Wagen gleich. Also berechnet man für den Wagen von rechts die Geschwindigkeitsdifferenz der 2. Phase zu 0.875 * 1.2 m/s = 1.05 m/s
- daraus ergibt sich eine Endgeschwindigkeit des Wagens von rechts von 0.8 m/s + 1.05 m/s = 1.85 m/s
- die maximale Fallhöhe des Impulses (zu Beginn des Stosses) beträgt 1.6 m/s - (-0.4 m/s) = 2.0 m/s und die max. Pumphöhe (am Ende des Stosses) erreicht einen Wert von 1.85 m/s - 0.1 m/s = 1.75 m/s. Die mittlere Fallhöhe beträgt hier die Hälfte, also 1 m/s, analog die mittlere Pumphöhe 0.875 m/s
- beim Fallen (1. Stossphase) fliesst ein Impuls von 0.8 m/s * 0.6 kg = 0.48 Ns, beim Pumpen (2. Stossphase) von 0.7 m/s * 0.6 kg = 0.42 Ns
Damit ist die Aufgabe gelöst:
- Am Schluss gleitet das leichtere Fahrzeug mit einer Geschwindigkeit von 1.85 m/s nach rechts.
- In der ersten Teilphase setzt der Impuls die folgende Energiemenge frei [math]W_{frei} = 0.48 Ns * 1 m/s = 0.48 J[/math] (geflossener Impuls mal mittlere Fallhöhe). In der zweiten Teilphase nimmt der Impuls einen Teil dieser Energie wieder zurück [math]W_{auf} = 0.42 Ns * 0.875 m/s = 0.368 J[/math].
Das Verhältnis der vom Impuls freigesetzten Energie zur vom Impuls wieder aufgenommenen ist gleich dem Quadrat des Verhältnis der zugehörigen Geschwinigkeitsänderungen.