Lösung zu Rollkörper auf schiefer Ebene: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Auf den Rollkörper wirken nur das Gravitationsfeld und die Unterlage ein. Die Wirkung des Gravitationsfeldes |
Auf den Rollkörper wirken nur das [[Gravitationsfeld]] und die Unterlage ein. Die Wirkung des Gravitationsfeldes (Stärke der [[Impulsquelle]]) heisst Gewichtskraft. Die Wirkung der Unterlage kann in eine [[Normalkraft]] und eine [[Gleitreibung|Haftreibungskraft]] zerlegt werden (die Rollreibung würde ein zusätzliches Drehmoment erzeugen). |
||
1. [[Bild:Schnittbild_Rollkoerper.png|thumb|Schnittbild (free body diagram)]] Das |
1. [[Bild:Schnittbild_Rollkoerper.png|thumb|Schnittbild (free body diagram)]] Das Schnittbild zeigt die drei Kräfte, die auf den Rollkörper einwirken. |
||
2. In der Ebene kann ein starrer Körper nur zwei "Sorten" [[Impuls]] und eine "Sorte" [[Drehimpuls]] mit der Umgebung austauschen. Kombiniert man die Bilanzgesetze mit den zugehörigen kapazitiven |
2. In der Ebene kann ein starrer Körper nur zwei "Sorten" [[Impuls]] und eine "Sorte" [[Drehimpuls]] mit der Umgebung austauschen. Kombiniert man die Bilanzgesetze mit den zugehörigen kapazitiven Gesetzen, erhält man die Grundgesetze der Mechanik |
||
:''x''-Impuls: <math>F_G |
:''x''-Impuls: <math>F_G\sin\beta-F_{HR}=\dot p_x=m\dot v_x</math> |
||
:''y''-Impuls: <math>F_G |
:''y''-Impuls: <math>F_G\cos\beta-F_N=\dot p_y=0</math> |
||
:''z''-Drehimpuls: <math> |
:''z''-Drehimpuls: <math>F_{HR}\cdot r=\dot L_z=J_z \dot \omega_z</math> |
||
Die ''y''-Bilanz muss beigezogen werden, wenn man prüfen will, ob die Bedingung bezüglich Rollen (maximal mögliche Haftreibungskraft) nicht verletzt wird. Nachfolgend werden die |
Die ''y''-Bilanz muss beigezogen werden, wenn man prüfen will, ob die Bedingung bezüglich Rollen (maximal mögliche Haftreibungskraft) nicht verletzt wird. Nachfolgend werden die Indizes x, y und z weggelassen. |
||
3.Die Rollbedingung verlangt, dass die Geschwindigkeit des Massenmittelpunktes gleich Winkelgeschwindigkeit mal Abrollradius ist. Leitet man diese Beziehung nach der Zeit ab, erhält man die analoge Aussage bezüglich Beschleunigung und Winkelbeschleunigung. Damit reduziert sich das Gleichungssystem auf |
3. Die Rollbedingung verlangt, dass die Geschwindigkeit des Massenmittelpunktes gleich Winkelgeschwindigkeit mal Abrollradius r ist. Leitet man diese Beziehung nach der Zeit ab, erhält man die analoge Aussage bezüglich Beschleunigung und Winkelbeschleunigung. Damit reduziert sich das Gleichungssystem auf |
||
:''x''-Impulsbilanz: <math>mg\sin |
:''x''-Impulsbilanz: <math>mg\sin\beta-F_{HR}=m\dot v</math> |
||
:''z''-Drehimpulsbilanz: <math> |
:''z''-Drehimpulsbilanz: <math>F_{HR}\cdot r=J\dot\omega=\frac{J}{r }\dot v</math> |
||
oder aufgelöst nach der Beschleunigung des Massenmittelpunktes |
oder aufgelöst nach der Beschleunigung des Massenmittelpunktes (die 2. Gleichung nach F<sub>HR</sub> auflösen und in die 1. Gleichung einsetzen, diese dann nach <math>\dot v</math> auflösen): |
||
:<math>\dot v = \frac {g}{k} \sin \beta</math> mit dem Faktor <math>k = 1 + \frac {J}{mr^2}</math> |
:<math>\dot v = \frac {g}{k} \sin \beta</math> mit dem Faktor <math>k = 1 + \frac {J}{mr^2}</math> |
||
| Zeile 22: | Zeile 22: | ||
Setzt man den Faktor ''k'' gleich eins, erhält man die Beschleunigung eines reibungsfrei gleitenden Körpers. |
Setzt man den Faktor ''k'' gleich eins, erhält man die Beschleunigung eines reibungsfrei gleitenden Körpers. |
||
4. Der Weg über die [[Energiebilanz]] ist schneller, liefert aber keine Informationen zu den Zwangskräften ([[ |
4. Der Weg über die [[Energiebilanz]] ist schneller, liefert aber keine Informationen zu den Zwangskräften ([[Normalkraft]] und [[Gleitreibung|Haftreibungskraft]]) |
||
:<math>\dot W_G |
:<math>\dot W_G+\dot W_{kin}+\dot W_{rot}=0, \quad W_G = m g h, \quad W_{kin} = \frac {m} {2} v^2, \quad W_{rot} = \frac {J}{2} \omega ^2</math> |
||
:<math>mg\dot h |
:<math>mg\dot h+mv\dot v+J\omega\dot\omega=0</math> |
||
Die Geschwindigkeit hängt mit der Änderungsrate der Höhe zusammen: <math> \dot h = -v\cdot sin\beta </math>. Mit Hilfe der Rollbedingung eliminiert man ω und seine Änderungsrate und erhält |
|||
:<math>mg\sin |
:<math>-mg\sin\beta v + mv\dot v+ J \frac{v\dot v}{r^2} = 0 </math> |
||
und daraus die |
und daraus dann die gleiche Formel wie oben. |
||
5. Die Kugel wird umso stärker beschleunigt, je kleiner der Faktor ''k'' ist, d.h. je weniger er von eins abweicht und je kleiner das Verhältnis des Massenträgheitsmoments zu Masse mal Quadrat des Abrollradius ''r'' ist. Mit dem Massenträgheitsmoment der Kugel J = 2/5 m R<sup>2</sup> und Kugelradius R wird |
|||
:<math> k = 1+\frac{2 R^2}{5 r^2}</math> |
|||
Die Kugel ist somit um so schneller, je weniger sich Abroll- und Kugelradius unterscheiden oder je kleiner die vom U-Profil gebildete "Spurweite" ist. Diese ist im Grenzfall 0 und beide Radien sind gleich. |
|||
'''[[Rollkörper auf schiefer Ebene|Aufgabe]]''' |
|||
Aktuelle Version vom 24. März 2016, 12:31 Uhr
Auf den Rollkörper wirken nur das Gravitationsfeld und die Unterlage ein. Die Wirkung des Gravitationsfeldes (Stärke der Impulsquelle) heisst Gewichtskraft. Die Wirkung der Unterlage kann in eine Normalkraft und eine Haftreibungskraft zerlegt werden (die Rollreibung würde ein zusätzliches Drehmoment erzeugen).
1.
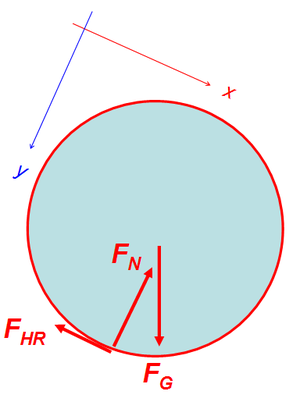
Das Schnittbild zeigt die drei Kräfte, die auf den Rollkörper einwirken.
2. In der Ebene kann ein starrer Körper nur zwei "Sorten" Impuls und eine "Sorte" Drehimpuls mit der Umgebung austauschen. Kombiniert man die Bilanzgesetze mit den zugehörigen kapazitiven Gesetzen, erhält man die Grundgesetze der Mechanik
- x-Impuls: [math]F_G\sin\beta-F_{HR}=\dot p_x=m\dot v_x[/math]
- y-Impuls: [math]F_G\cos\beta-F_N=\dot p_y=0[/math]
- z-Drehimpuls: [math]F_{HR}\cdot r=\dot L_z=J_z \dot \omega_z[/math]
Die y-Bilanz muss beigezogen werden, wenn man prüfen will, ob die Bedingung bezüglich Rollen (maximal mögliche Haftreibungskraft) nicht verletzt wird. Nachfolgend werden die Indizes x, y und z weggelassen.
3. Die Rollbedingung verlangt, dass die Geschwindigkeit des Massenmittelpunktes gleich Winkelgeschwindigkeit mal Abrollradius r ist. Leitet man diese Beziehung nach der Zeit ab, erhält man die analoge Aussage bezüglich Beschleunigung und Winkelbeschleunigung. Damit reduziert sich das Gleichungssystem auf
- x-Impulsbilanz: [math]mg\sin\beta-F_{HR}=m\dot v[/math]
- z-Drehimpulsbilanz: [math]F_{HR}\cdot r=J\dot\omega=\frac{J}{r }\dot v[/math]
oder aufgelöst nach der Beschleunigung des Massenmittelpunktes (die 2. Gleichung nach FHR auflösen und in die 1. Gleichung einsetzen, diese dann nach [math]\dot v[/math] auflösen):
- [math]\dot v = \frac {g}{k} \sin \beta[/math] mit dem Faktor [math]k = 1 + \frac {J}{mr^2}[/math]
Setzt man den Faktor k gleich eins, erhält man die Beschleunigung eines reibungsfrei gleitenden Körpers.
4. Der Weg über die Energiebilanz ist schneller, liefert aber keine Informationen zu den Zwangskräften (Normalkraft und Haftreibungskraft)
- [math]\dot W_G+\dot W_{kin}+\dot W_{rot}=0, \quad W_G = m g h, \quad W_{kin} = \frac {m} {2} v^2, \quad W_{rot} = \frac {J}{2} \omega ^2[/math]
- [math]mg\dot h+mv\dot v+J\omega\dot\omega=0[/math]
Die Geschwindigkeit hängt mit der Änderungsrate der Höhe zusammen: [math] \dot h = -v\cdot sin\beta [/math]. Mit Hilfe der Rollbedingung eliminiert man ω und seine Änderungsrate und erhält
- [math]-mg\sin\beta v + mv\dot v+ J \frac{v\dot v}{r^2} = 0 [/math]
und daraus dann die gleiche Formel wie oben.
5. Die Kugel wird umso stärker beschleunigt, je kleiner der Faktor k ist, d.h. je weniger er von eins abweicht und je kleiner das Verhältnis des Massenträgheitsmoments zu Masse mal Quadrat des Abrollradius r ist. Mit dem Massenträgheitsmoment der Kugel J = 2/5 m R2 und Kugelradius R wird
- [math] k = 1+\frac{2 R^2}{5 r^2}[/math]
Die Kugel ist somit um so schneller, je weniger sich Abroll- und Kugelradius unterscheiden oder je kleiner die vom U-Profil gebildete "Spurweite" ist. Diese ist im Grenzfall 0 und beide Radien sind gleich.