Widerstand einer Glühbirne: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
#Wie stark ist der Strom bei der Betriebsspannung von 12 V |
#Wie stark ist der Strom bei der Betriebsspannung von 12 V |
||
#Wie gross ist die Leistung bei 5, 10 und 14 V? |
#Wie gross ist die Leistung bei 5, 10 und 14 V? |
||
#Wie heiss ist der Wolframdraht der Glühbirne bei 5, 10 und 14 V? Gehen Sie davon aus, dass der Wolframwiderstand quadratisch von der Temperatur abhängt: <math>R=R_{20}(1+\alpha\Delta T+\beta(\Delta T)^2)</math>, Werte der Koeffizienten siehe unten. Der Wert R<sub>20</sub> ist der Widerstand bei der Referenztemperatur von 20°C. Den kann man aus der Kennlinie herauslesen. <math>\Delta T</math> ist die Temperaturdifferenz des Drahtes zur Referenztemperatur. |
|||
#Wie heiss ist der Wolframdraht der Glühbirne bei 5, 10 und 14 V? |
|||
#Die Abstrahlungsleistung nimmt mit der absoluten Temperatur (Temperatur in Grad Celsius plus 273) hoch vier zu. |
#Die Abstrahlungsleistung nimmt mit der absoluten Temperatur (Temperatur in Grad Celsius plus 273) hoch vier zu. Tragen Sie die drei berechneten Leistungen gegen die 4. Potenz der absoluten Temperatur auf und überprüfen Sie, ob eine Gerade herauskommt. |
||
'''Daten von Wolfram:''' |
'''Daten von Wolfram:''' |
||
{| |
{| |
||
|width=" |
|width="250"|spezifischer Widerstand |
||
|width="150"|5.6 10<sup>-8</sup> Ωm |
|width="150"|5.6 10<sup>-8</sup> Ωm |
||
|- |
|- |
||
|linearer Temperaturkoeffizient |
|linearer Temperaturkoeffizient <math>\alpha</math> |
||
|4.11 10<sup>-3</sup> /°C |
|4.11 10<sup>-3</sup> /°C |
||
|- |
|- |
||
|quadratischer Temperaturkoeffizient |
|quadratischer Temperaturkoeffizient <math>\beta</math> |
||
|9.62 10<sup>-7</sup> /°C |
|9.62 10<sup>-7</sup> /°C |
||
|} |
|} |
||
'''[[Resultate zu Widerstand einer Glühbirne|Resultate]]''' |
|||
'''[[Lösung zu Widerstand einer Glühbirne|Lösung]]''' |
'''[[Lösung zu Widerstand einer Glühbirne|Lösung]]''' |
||
'''[https://www.youtube.com/watch?v=c25Gk35oUHs Video mit SD-Modell]''' |
|||
| ⚫ | |||
| ⚫ | |||
Aktuelle Version vom 3. Mai 2016, 10:08 Uhr
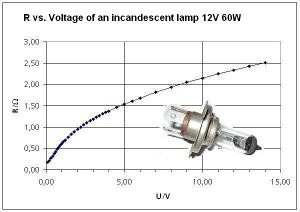
Die Graphik zeigt die Widerstands-Spannungs-Kennlinie einer Glühbirne.
- Wie stark ist der Strom bei der Betriebsspannung von 12 V
- Wie gross ist die Leistung bei 5, 10 und 14 V?
- Wie heiss ist der Wolframdraht der Glühbirne bei 5, 10 und 14 V? Gehen Sie davon aus, dass der Wolframwiderstand quadratisch von der Temperatur abhängt: [math]R=R_{20}(1+\alpha\Delta T+\beta(\Delta T)^2)[/math], Werte der Koeffizienten siehe unten. Der Wert R20 ist der Widerstand bei der Referenztemperatur von 20°C. Den kann man aus der Kennlinie herauslesen. [math]\Delta T[/math] ist die Temperaturdifferenz des Drahtes zur Referenztemperatur.
- Die Abstrahlungsleistung nimmt mit der absoluten Temperatur (Temperatur in Grad Celsius plus 273) hoch vier zu. Tragen Sie die drei berechneten Leistungen gegen die 4. Potenz der absoluten Temperatur auf und überprüfen Sie, ob eine Gerade herauskommt.
Daten von Wolfram:
| spezifischer Widerstand | 5.6 10-8 Ωm |
| linearer Temperaturkoeffizient [math]\alpha[/math] | 4.11 10-3 /°C |
| quadratischer Temperaturkoeffizient [math]\beta[/math] | 9.62 10-7 /°C |