Lösung zu Mantelstromtriebwerk: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Bild:Mantelstromtriebwerk.png]] |
[[Bild:Mantelstromtriebwerk.png]] |
||
Die Impulsbilanz bezüglich des Triebwerkes lautet unter Vernachlässigung der Druckkräfte |
Die Impulsbilanz bezüglich des Triebwerkes lautet unter Vernachlässigung der Druckkräfte, bei stationärem Betrieb und mit Bezugsrichtung = Flugrichtung |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | Die Kraft des Flugzeug auf das Triebwerk '''''F<sub>F</sub>''''' weist gegen hinten, die zugehörige Reaktionskraft auf das Flugzeug, der Schub, gegen vorne. Die Impulsänderungsrate ist 0 wegen des stationären Betriebs. Mit v<sub>D</sub> = 2 * v<sub>i</sub>, v<sub>M</sub> = 1.25 * v<sub>i</sub>, I<sub>mD</sub> = 0.2 * I<sub>mi</sub> und I<sub>mM</sub> = 0.8 * I<sub>mi</sub> ergibt das: |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Da alle Geschwindigkeiten, aber nur die austretenden Massenströme negativ sind, bleiben deren Produkte positiv: |
|||
| ⚫ | |||
Damit erhält man für die Schubkraft |
Damit erhält man für die Schubkraft |
||
:<math>F_{Schub} = |
:<math>F_{Schub} = F_F = 0.4 \cdot v_i \cdot I_{mi}</math> = 66.76 kN |
||
Aktuelle Version vom 4. März 2010, 17:54 Uhr
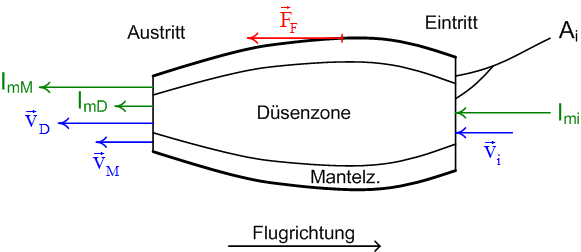
Die Impulsbilanz bezüglich des Triebwerkes lautet unter Vernachlässigung der Druckkräfte, bei stationärem Betrieb und mit Bezugsrichtung = Flugrichtung
- [math]-F_F + I_{mi} \cdot (-v_i) - I_{mD} \cdot (-v_D) - I_{mM} \cdot (-v_M) = \dot p = 0[/math],
wobei für die Geschwindigkeiten die Beträge eingesetzt werden und der durchgepumpte Massenstrom die folgende Stärke aufweist
- [math]I_{mi} = \rho v_i A_i[/math] = 0.85 kg/m3 * 250 m/s * π/4 * (2 m)2 = 667.6 kg/s.
Die Kraft des Flugzeug auf das Triebwerk FF weist gegen hinten, die zugehörige Reaktionskraft auf das Flugzeug, der Schub, gegen vorne. Die Impulsänderungsrate ist 0 wegen des stationären Betriebs. Mit vD = 2 * vi, vM = 1.25 * vi, ImD = 0.2 * Imi und ImM = 0.8 * Imi ergibt das:
- [math]-F_F - I_{mi} \cdot v_i + 0.2 \cdot I_{mi} \cdot 2 \cdot v_i + 0.8 \cdot I_{mi} \cdot 1.25 \cdot v_i = 0[/math]
Damit erhält man für die Schubkraft
- [math]F_{Schub} = F_F = 0.4 \cdot v_i \cdot I_{mi}[/math] = 66.76 kN