Gravitation als Impulsquelle

Die Gravitation ist für uns Menschen allgegenwärtig. Solange wir uns nicht in einem Fahr- oder Flugzeug befinden, wissen wir jederzeit, wo oben und unten ist. Ursache dieses Phänomens ist die permanente Wirkung des Gravitationsfeldes. Dieses Feld pumpt - bei einer nach unten gerichteten Bezugsrichtung - andauernd Impuls in unseren Körper hinein. Uns bleiben dann nur noch zwei Möglichkeiten, zu fallen oder den Impuls unmittelbar an die Erde abzuführen. Solange wir fallen, spüren wir von der Gravitation überhaupt nichts mehr. Dafür bezahlen wir diese Schwerelosigkeit im schlimmsten Fall mit dem Leben, nämlich dann, wenn wir den Impuls beim Aufprall blitzartig nach unten abgeben müssen.

Die Stärke der gravitativen Impulsquelle, die Gewichtskraft, ist proportional zu Masse m und proportional zur Gravitationsfeldstärke g. Die Masse ist demnach eine Doppeleigenschaft der Materie. Einerseits wirkt sie als Kapazität bezüglich der Grösse Impuls (träge Masse), andererseits legt sie zusammen mit dem Gravitationsfeld die Stärke der Gewichtskraft fest (schwere Masse). Diese Doppeleigenschaft ist dafür verantwortlich, dass ein Pilot in seinem Cockpit nicht zwischen der "echten" Gravitation und der Beschleunigung des Flugzeuges unterscheiden kann.

Lernziele

In dieser Vorlesung lernen Sie

• dass ein Körper in seinem Innern Impuls mit dem Gravitationsfeld austauscht (Volumenkraft)
• wie die Gravitation bei eindimensionaler Bewegung ins Flüssigkeitsbild eingebaut wird
• wie die Stärke des Gravitationsfeldes bei einem Himmelskörper berechnet wird
• wie die Impulsbilanz bezüglich eines Körpers allgemein formuliert wird
• dass in jedem beschleunigten System ein Trägheitsfeld wirkt
• wie das Gravitationsfeld in einem beschleunigten Bezugssystem zu rechnen ist
• was man heute unter Schwerelosigkeit versteht

Impulsquelle

Wassertropfen als Impulsspeicher

Ein Tropfen, der am Wasserhahn hängt, gibt den vom Gravitationsfeld zugeführten Impuls direkt nach oben ab. Der rückwärts fliessende Impulsstrom belastet das Wasser auf Zug, wodurch die typische Tropfenform entsteht (der Impulstransport durch das Wasser erfolgt wie bei einem aufgehängten Mehlsack hauptsächlich über die Oberfläche). Sobald sich der Tropfen vom Hahn löst, bleibt der Impuls dort liegen, wo er zugeführt wird, d.h. jedes Wassermolekül sammelt den Impuls, den es vom Gravitationsfeld bekommt. Weil dann keine Impulsströme mehr durch das Wasser fliessen, ist der Tropfen praktisch spannungsfrei. Einzig die Oberflächenspannung, die den Tropfen zu einer Kugel formt, und der Luftwiderstand stören diesen Zustand der Schwerelosigkeit. Mit dem Aufschlag gibt der Tropfen den in der Zwischenzeit gesammelten Impuls schlagartig an den Boden ab. Fällt der Tropfen ins Wasser, gibt er mehr Impuls ab, als er besitzt. Deshalb taucht er danach mindestens noch einmal auf.

Die Impulsquellen bestimmen unsern Alltag. Ob wir stehen, sitzen oder liegen, immer muss der gravitativ zufliessende Impuls nach unten an die Erde abgegeben werden. Die dadurch ausgelösten Impulsströme belasten unser Skelett beim Stehen und führen bei längerem Liegen zu Druckgeschwüren (Dekubitus). Viele Pflanzen leiden noch stärker unter der Gravitation als der Mensch. Damit eine Fichte im dichten Wald genügend Licht erhält, muss sie möglichst hoch wachsen. Dadurch vergrössert sich ihre Masse und damit die Stärke der Impulsquelle. Am Bauplan der Fichte kann man erkennen, wie die Natur solche statischen Probleme löst. Der genau vertikal ausgerichtete Stamm wird nach unten immer dicker und kann so die von den Ästen zufliessenden Impulsströme sammeln und nach gegen den Boden ableiten. Kein Zufall, dass alle hohen und schlanken Gebäude wie der Eiffelturm oder ein Fernsehturm eine ähnliche Geometrie aufweisen wie der Stamm einer Fichte.

In Brücken, Dachstühlen und Strommasten kommt noch ein weiteres Problem dazu. In diesen Bauwerken wird der gravitativ zugeführte Impuls seitwärts abgeleitet. Nun kann man den Impulsstrom mehr oder weniger problemlos vorwärts (Druck) oder rückwärts (Zug) durch ein Bauteil hindurch führen. Sobald man aber eine Impuskomponente seitwärts zur Bezugsrichtung ableiten will, entstehen im dafür vorgesehenen Bauteil zusätzliche Wirbelströme, die das Material extrem belasten. In der Rotationsmechanik werden wir dieses Phänomen von einer etwas höheren Warte aus betrachten und dabei feststellen, dass ein seitwärts fliessender Impulsstrom als Quelle für die mengenartige Grösse Drehimpuls wirkt.

Flüssigkeitsbild

Wurf nach oben im Flüssigkeitsbild

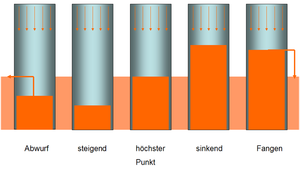
Bewegungen längs einer Geraden lassen sich mit grossem Gewinn im Flüssigkeitsbild darstellen. Die Geometrie der Anordnung geht in diesem Bild weitgehend verloren, dafür wird die ganze Dynamik mit Impuls und Energie sichtbar gemacht. Untersucht man Bewegungen in vertikaler Richtung, muss noch die Wirkung des Gravitationsfeldes ins Bild eingebaut werden. Weil die Masse, die Grundfläche der Töpfe, für die Stärke der gravitativen Impulsquelle verantwortlich ist, fügt man die die Gewichtskraft als Dauerregen ins Flüssigkeitsbild ein. Die Regendichte entspricht dann der Gravitationsfeldstärke.

Ein Körper bewegt sich nach oben, falls sein Impuls negativ ist. Stellt man den Abwurf im Flüssigkeitsbild dar, wird so lange Impuls aus dem Topf gepumpt, bis dessen Oberfläche weit unter den Spiegel des Sees zu liegen kommt. Dank des gravitativen Dauerregens steigt der Spiegel im Topf kontinuierlich an. Es ist nun leicht einzusehen, dass die Regendichte (Impuls pro Zeit und Masse) der Geschwindigkeit des Spiegels im Topf (Beschleunigung) entspricht. Wirft man mehrere Körper gleichzeitig hoch, erhält man im Flüssigkeitsbild eine ganze Sammlung von Töpfen, die alle mit gleicher, negativer Füllhöhe starten. Weil die grossen Töpfe mehr Impuls pro Zeit aufnehmen (schwere Masse), aber auch mehr Impuls pro Geschwindigkeit speichern können (träge Masse), steigt das Niveau in allen Töpfen gleich schnell. Die im Vakuum hoch geworfenen Massen haben zu jeder Zeit die gleiche Geschwindigkeit und behalten ohne gegenseitige Beeinflussung ihren gegenseitigen Abstand bei. Packt man nun alle Körper in einen Kasten ein, bleiben sie während des Flugs relativ zu diesem Kasten in der Schwebe. Während de Freiflugphase, dann wenn nur das Gravitationsfeld wirkt, herrscht im Kasten Schwerelosigkeit.

Gravitationsfeld eines Himmelskörpers

Feld von Erde und Mond

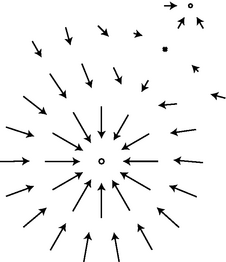
Das Gravitationsfeld wirkt nicht nur auf die Körper ein. Es wird von diesen auch aufgebaut. Massive Körper wie die Sonne, die Erde oder der Mond erzeugen in ihrer Umgebung ein starkes Gravitationsfeld. Dieses Feld verdünnt sich analog zum elektrischen Feld der geladenen Metallkugel. In der Vorlesung Ladung und Strom haben Sie gehört, dass das elektrische Feld einer geladenen Kugel mit dem Quadrat des Abstandes von der Kugelmitte abnimmt

[math]E(r)=\frac{1}{4\pi\varepsilon_0}\frac{Q}{r^2}[/math]

Das Gravitationsfeld einer massiven Kugel hat eine dazu analoge Gestalt

[math]g(r)=G\frac{m}{r^2}[/math]

G ist die universell gültige Gravitationskonstante und hat den Wert 6.67 10^-11 m³/(kgs²). Die Gravitationskonstante beschreibt, wie stark das von einer einzelnen Masse erzeugte Feld bei gegebenem Abstand ist. Nimmt man eine Kugel mit der Masse von einem Kilogramm, dann entspricht die Feldstärke in einem Meter Abstand von der Kugelmitte zahlenmässig der Gravitationskonstante (g = 6.67 10^-11 N/kg).

Ein elektrisches Feld kann positiv und negativ geladen sein. Bei positiv geladenen Körpern zeigt die Feldstärke radial nach aussen. Die Formel für das Feld einer geladenen Kugel lautet demnach

[math]\vec E(r)=\frac{1}{4\pi\varepsilon_0}\frac{Q}{r^3}\vec r[/math]

Falls die Ladung der Metallkugel Q negativ ist, zeigt der Vektor E gegen r, also nach innen. In der klassischen Physik kennt man nur positive Massen. Zudem zeigt die Gravitationsfeldstärke immer gegen den Himmelskörper

[math]\vec g(r)=-G\frac{m}{r^3}\vec r[/math]

Fasst man die Felderzeugung und die Feldwirkung (Gewichtskraft, Stärke der Impulsquelle)

[math]\vec F_G=m\vec g[/math]

zusammen, erhält man das alte Wechselwirkungsgesetz von Isaac Newton. So erzeugt die Erde am Ort des Mondes eine bestimmte Feldstärke und der Mond am Ort der Erde eine deutlich schwächere. Multipliziert man die jeweilige Feldstärke mit der Masse des dort befindlichen Körpers, erhält man die Stärke des zwischen den beiden Körpern fliessenden Impulsstromes

[math]F_{G_{Mond}}=m_{Mond}\cdot g_{Erde}=G\frac{m_{Mond}\cdot m_{Erde}}{r^2}=m_{Erde}\cdot g_{Mond}=F_{G_{Erde}}[/math]

Zwischen Erde und Mond fliesst ein gewaltiger Impulsstrom. Wo dieser Impuls zwischen Erde und Monde überall durchfliesst, lässt sich bis heute nicht mit Bestimmtheit sagen.

Impulsbilanz

Impulsabfluss über Waage und Wederwaage

Das Gewicht ist eine ganz spezielle Kraft. Im Gegensatz zu den Stärken der durch die Körperoberfläche fliessenden Impulsströme, den Oberflächenkräften, beschreibt die Gewichtskraft den volumenmässigen Impulstausch zwischen Körper und Gravitationsfeld. Deshalb nennt man die Gewichtskraft oft auch Volumenkraft. Um die Gewichtskraft klar gegen die eigentlichen Impulsströme abzugrenzen, schreiben wir die beiden Arten des Impulsaustausches getrennt in die Bilanz hinein

[math]\sum_i \vec F_i+\vec F_G=\dot{\vec p}[/math]

Nun ersetzen wir die Gewichtskraft durch die Wirkung des Gravitationsfeldes und den Impulsinhalt durch das kapazitive Gesetz

[math]\sum_i \vec F_i+m\vec g=m\dot{\vec v}=m\vec a[/math]

Auf der linken Seite der Gleichung steht m für die schwere und rechts für die träge Masse.

Solange man die Körper nur als materielle Punkte sieht, macht die Unterscheidung zwischen Volumen- und Oberflächenkraft wenig Sinn. Für das Verständnis realer Objekte ist aber die Frage, wie der Impuls durch die einzelnen Körper fliesst, von zentraler Bedeutung. Unser eigener Körper ist so gebaut, dass der gravitativ zugeführte Impuls mit Vorteil auf dem direktem Weg nach unten abgeführt wird. Wir können problemlos einige Minuten am gleichen Ort stehen bleiben, haben aber gross Mühe, uns am Balkon hängend über längere Zeit festzuhalten.

Trägheitsfeld

Ein Körper kann den Impuls leitungsartig über die Oberfläche und quellenartig über das Volumen austauschen. Zudem ist für die Impulsquelle die gleiche physikalische Grösse verantwortlich wie für die Impulsspeicherung, nämlich die Masse. Diese doppelte Wirkung der Masse gilt auch lokal: ein inhomogener Körper speichert dort am meisten Impuls, wo er die stärkste Impulsquelle hat. Wirft man zum Beispiel eine Hantel, bestehend aus zwei Bleikugeln und einem Verbindungsrohr aus Aluminium hoch, fliessen während des Wurfs im Innern der Hantel keine Impulsströme, weil die Bleikugeln pro Volumen mehr Impuls aufnehmen, aber auch entsprechend mehr Impuls speichern können. Lässt man diese Hantel im evakuierten Fallturm von Bremen fallen, bleibt die Hantel während des Falls spannungsfrei, weil keine ausgleichenden Impulsströme fliessen müssen.

Die doppelte Wirkung der Masse hindert uns daran, den Unterschied zwischen einem Gravitationsfeld und einem beschleunigten Bezugssystem zu erkennen. Auf der Erdoberfläche tauscht jeder Körper mit dem Gravitationsfeld Impuls aus. Diese Impulsquellen, deren Stärke mit Masse mal Gravitationsfeldstärke angegeben werden kann, belasten Menschen, Tiere, Pflanzen und Gebäude gleichermassen. Alle Objekte müssen den gravitativ zufliessenden Impuls leitungsartig wieder an die Erde abgeben. Nur wer frei fällt, kann sich dieser Belastung entziehen. Wenn wir in einem Raumschiff sässen, das weit weg von allen Himmelskörpern mit 9,81 m/s² beschleunigt würde, hätten wir das Gefühl, auf der Erdoberfläche zu sein. Unser Körper, der Stuhl auf dem wir sitzen und die Lampe, die uns Licht spendet, wären dann von den gleichen Impulsströmen durchflossen wie in einem ruhenden Zimmer auf der Erdoberfläche.

Gravitationsfeld in einem startenden Flugzeug

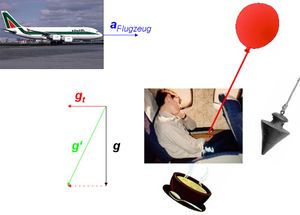
Mathematisch lässt sich diese Doppelbödigkeit von Gravitation und Beschleunigung leicht durchschauen. Betrachten wir dazu einen Passagier in einem startenden Flugzeug. Von der Piste aus gesehen wirkt neben der Gewichtskraft nur noch der Sitz auf den Menschen ein. Die Resultierende aus Sitzkraft und Gewichtskraft führen dem Passagier soviel Impuls zu, wie er braucht, um die Beschleunigung des Flugzeuges mitzumachen

[math]\vec F_S+\vec F_G=\dot{\vec p}[/math]

Nun sind sowohl die Gewichtskraft als auch die Impulsänderungsrate proportional zur Masse

[math]\vec F_S+m\vec g=m\vec a_{Flugzeug}[/math]

Der Passagier sieht wohl, dass sich die Piste immer schneller nach hinten schiebt, spürt aber vor allem, dass er von unsichtbarer Hand nach hinten gedrückt wird. Relativ zum Flugzeug stellt der Passagier ein veräntertes Gravitationsfeld fest (stärker und anders gerichtet)

[math]\vec F_S+m(\vec g-\vec a_{Flugzeug})=\vec F_S+m(\vec g+\vec g_t)=\vec F_S+m \vec g_{Flugzeug}=0[/math]

Der Passagier ist relativ zum Flugzeug in Ruhe, empfindet dafür ein stärkeres Gravitationsfeld als vor dem Start. Die neue Gravitationsfeldstärke ist gleich der alten plus die Stärke eines Trägheitsfeldes. Die Stärke des Trägheitsfeldes ist gleich minus die Beschleunigung des Flugzeuges. Das überlagerte Feld, bestehend aus altem Gravitationsfeld und Trägheitsfeld, beeinflusst alle Phänomene im Flugzeug drin. Die Oberfläche des Tees in der Tasse stellt sich normal zur neuen Gravitationsfeldstärke ein, die Schnur eines Kinderballons verläuft längs den neuen Feldlinien und ein losgelassener Körper fällt entlang dem neuen Lot. Zudem ist die Beschleunigung des fallenden Körpers relativ zum Flugzeug gleich der Stärke des neuen Gravitationsfeldes,also gleich

[math]a=\sqrt{g^2+a_{Flugzeug}^2}[/math]

Diese Relativität von beschleunigtem Bezugssystem und Gravitation hat Einstein in den Rang einer grundlegenden Hypothese erhoben. Man kann mit keiner Messung entscheiden, ob ein Gravitationsfeld von einer Masse oder von einem beschleunigten Bezugssystem erzeugt wird. Deshalb dürfen wir von irgend einem System, das stabil genug ist, ausgehen und bedenkenlos in ein zweites wechseln. Die Gravitationsfeldstärke im zweiten System ist dann gleich Feldstärke im ersten minus die Beschleunigung es zweiten gemessen im ersten

[math]\vec g_{neu}=\vec g_{alt}+\vec g_t=\vec g_{alt}-\vec a_{rel}[/math]

Der Teil der Gewichtskraft im neuen System, der durch das Trägheitsfeld erzeugt wird, heisst auch Trägheitskraft

[math]\vec F_T=m\vec g_t=-m\vec a_{rel}[/math]

Von einer Trägheitskraft kann man demnach nur reden, wenn zwei verschiedene Systeme bekannt sind. Normalerweise sind das die Erde und ein relativ dazu beschleunigtes System wie etwa ein Karussell, ein Eisenbahnwagen oder eben ein Flugzeug.

Schwerelosigkeit

Libelle einer Wasserwaage

Wirkt nur die Gewichtskraft auf eine Kabine und die sich darin befindenden Körper ein, herrscht Schwerelosigkeit. Das Gravitationsfeld wird durch die Fallbewegung wegtransformiert und ist nicht mehr nachweisbar

[math]\vec g_{neu}=\vec g_{alt}+\vec g_t=\vec g_{alt}-\vec a_{rel}=\vec g_{alt}-\vec g_{alt}=0[/math]

Schwerelosigkeit bedeutet demnach nur, dass sich ein Körper im freien Fall befindet. Von einer absoluten und einer relativen Schwerelosigkeit zu sprechen, macht heute keinen Sinn mehr. In den weiten des Weltalls gibt es weder Ruhe, Geschwindigkeit noch Beschleunigung. Entweder sind die Triebwerke ausgeschaltet und im Raumschiff herrscht Schwerelosigkeit, oder die Triebwerke laufen und man misst relativ zum Raumschiff ein Gravitatationsfeld. Lässt man eine Raumstation rotieren, baut sich ein Zentrifugalfeld auf. Nur sind im rotierenden Bezugssystem die Verhältnisse noch etwas komplexer, weil neben der statischen Zentrifugalkraft noch eine geschwindigkeitsabhängige Corioliskraft auftritt.

Ein Astronaut ist schwerelos, weil sich sein Schiff im freien Fall befindet. Die Form seiner Bahn spielt dabei keine Rolle. Er kann auf einer Ellipes um die Erde fallen oder auf einer S-förmigen Kurve gegen den Mond fliegen. In der Kapsel herrscht Schwerelosigkeit, sobald die Triebwerke ausgeschaltet werden. Schwerelosigkeit kann heute auch auf der Erde erzeugt werden. Dazu lässt man eine Kapsel im Fallturm fallen oder man durchfliegt mit einem Flugzeug die Bahn eines im Vakuum geworfenen Körpers. Schiesst man die Kapsel im Fallturm zuerst hoch, verlängert sich die Zeit des schwerelosen Zustandes auf das Doppelte. Es spielt eben keine Rolle, ob sich die Kapsel nach oben oder unten bewegt. Entscheidend ist nur, dass ausser der Gewichtskraft keine weiteren Einflüsse vorhanden sind. Solange der Impuls dort gespeichert wird, wo er zufliesst, gibt es im Innern der Körper keine Ausgleichsströme. Und genau diesen Zustand nennt man schwerelos.

Kontrollfragen

1. Wieso ist die Gewichtskraft (Gravitationskraft oder Schwerkraft) eine besondere Kraft?
2. Wovon hängt die Stärke der Gewichtskraft ab?
3. Wie durchströmt der Vertikalimpuls eine an zwei Seilen aufgehängte Strassenlampe (Bezugsrichtung nach unten)?
4. Wie stark ist das Gravitationsfeld an einem Punkt, der sich einen Erdradius über der Erdoberfläche (etwa 6370 km) befindet?
5. Wieso ist ein Astronaut auf dieser Höhe dennoch schwerelos?
6. Ein Flugzeug startet mit einer Beschleunigung von 3 m/s²
   1. Welchen Winkel schliesst die Oberfläche einer mit fliegenden Flüssigkeit und die Piste ein?
   2. Wie richtet sich die Schnur eines mit Helium gefüllten Ballons aus?
   3. Welche Beschleunigung erfährt ein fallen gelassener Körper relativ zum Flugzeug?
7. Wie erzeugt man Schwerelosigkeit auf der Erde?

Lösungen zu den Kontrollfragen

1. Die Schwerkraft ist eine Volumenkraft, die zudem noch von der körpereigenen Grösse Masse abhängt.
2. Die Geschichts-, Schwer- oder Gravitationskraft ist proportional zur Masse (körpereigene Grösse) und proportional zu Stärke des Gravitationsfeldes (raumspezifische Grösse).
3. Die z-Komponente des Impulses wird vom Gravitationsfeld in die Lampe eingebracht. Von dort fliesst der Impuls über beide Seile seitwärts weg.
4. Vordoppelt man die Distanz zum Zentrum der Erde, schwächt sich das Gravitationsfeld auf einen Viertel ab.
5. Schwerelosigkeit tritt nicht dann auf, wenn das Gravitationsfeld verschwindet, sondern dann wenn das entsprechende System frei fällt.
6. Im Flugzeug misst man ein Gravitationsfeld, dessen vertikale Komponenten gleich 9.81 N/kg und dessen horizontale gleich 3 N/kg ist.
   1. Die Flüssigkeit neigt sich um 17° gegen die Piste nach hinten.
   2. Die Schnur des Ballons steht auch im Flugzeug normal zum Spiegel einer Flüssigkeit. Durch die Beschleunigung des Flugzeuges neigt sich die Schnur des Ballons um 17° nach vorn.
   3. Ein in diesem Flugzeug fallen gelassener Körper bewegt sich Lotrecht nach unten, d.h. er bewegt sich parallel zur Schnur des Ballons. Vernachlässigt man die Wirkung der Luft, beträgt seine Beschleunigung 10.26 m/s².
7. Schwerelosigkeit erzeugt man durch eine reine Fallbewegung (Fallturm, Parabelflug).

Materialien

• Skript Seite 14
• Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 96 und 97
• Videoaufzeichnung
• Kurzfassung auf Youtube

Physik und Systemwissenschaft in Aviatik 2014

Physik und Systemwissenschaft in Aviatik