Ungleiches Gleichgewicht: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 29. Februar 2016, 10:47 Uhr

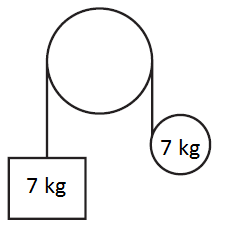
Über eine starr fixierte, also nicht drehbare Führungsrolle, kann ein ideales Seil reibungsfrei gleiten. An einem Ende des Seils hängt ein Klotz (Masse 7 kg). Das andere Ende ist um einen homogenen Zylinder (Masse 7 kg, Radius 5 cm) geschlungen und so befestigt, dass das Seil nicht rutschen kann.

Wie bewegen sich die beiden Körper nach dem Loslassen?

beide «fallen» gleich schnell
beide «fallen» , aber Zylinder «fällt» schneller als der Klotz
beide «fallen», aber Klotz «fällt» schneller als Zylinder
Zylinder bleibt stehen, Klotz «fällt»
Klotz bleibt stehen, Zylinder «fällt»
es passiert gar nichts, beide Körper bleiben ruhig hängen

Berechnen Sie Beschleunigung des Klotzes sowie Beschleunigung und Winkelbeschleunigung des Zylinders.
Wie gross sind die Seilkräfte?

Resultate

Lösung

Lösungsvideo

@@ Zeile 1: / Zeile 1: @@
-Über eine starr fixierte, also nicht drehbare Führungsrolle, kann ein ideales Seil reibungsfrei gleiten. An einem Ende des Seils hängt ein Klotz (Masse 7 kg). Das andere Ende ist um einen homogenen Zylinder (Masse 7 kg, Radius 5 cm) geschlungen und so befestigt, dass das Seil nicht rutschen kann.
+[[Datei:Klotz Walze Umlenkrolle.png|thumb|Was passiert hier?]]Über eine starr fixierte, also nicht drehbare Führungsrolle, kann ein ideales Seil reibungsfrei gleiten. An einem Ende des Seils hängt ein Klotz (Masse 7 kg). Das andere Ende ist um einen homogenen Zylinder (Masse 7 kg, Radius 5 cm) geschlungen und so befestigt, dass das Seil nicht rutschen kann.
 ::Wie bewegen sich die beiden Körper nach dem Loslassen?
 ::*beide «fallen» gleich schnell
@@ Zeile 15: / Zeile 15: @@
 '''[http://www.youtube.com/watch?v=L0agzNEEU8E Lösungsvideo]'''
+[[Kategorie:Rot]] [[Kategorie:Aufgaben]] [[Kategorie:RotAuf]] [[Kategorie:UebAV]]