Aviatik 2016/1

Erlaubte Hilfsmittel: Netzunabhängiger und nicht kommunikationsfähiger Taschenrechner, selbst verfasste Formel-, Modell- und Beispielsammlung mit maximal 7 Seiten (7 einseitig oder 3.5 zweiseitig beschriebene Blätter), Wörterbuch für fremdsprachige Studierende.

Aufgabe 1

Aufgabe 1: zwei Gefässe

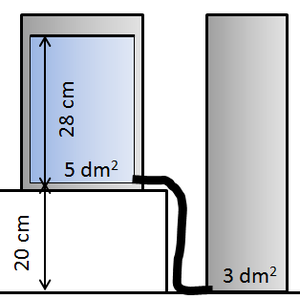
Ein zylinderförmiges Gefäss (Querschnitt 5 dm²) ist 28 cm hoch mit Wasser gefüllt. Dieses Gefäss ist über einen Schlauch mit einem zweiten Gefäss (Querschnitt 3 dm²) verbunden, das anfänglich leer ist. Der Boden des zweiten Gefässes liegt 20 cm unterhalb des Bodens des ersten Gefässes. Nach 150 Sekunden sind die Spiegel in den beiden Gefässen angeglichen.

1. Wie hoch ist das zweite Gefäss nach 150 Sekunden mit Wasser gefüllt und wieviel Energie wird in diesen 150 insgesamt dissipiert?
2. Man beobachtet, dass die Volumenstromstärke linear mit der Zeit abnimmt. Wie gross ist die Volumenstromstärke zum Zeitpunkt 100 Sekunden?
3. Skizzieren Sie ein Systemdiagramm (Flowchart) für dieses System (ohne Energieebene).
4. Schreiben Sie alle notwendigen Gleichungen ins Systemdiagramm hinein (nur turbulente Reibung). Wie gross ist der turbulente Widerstand k_V, den Sie ins Modell einsetzen?

Aufgabe 2

In der nebenstehend skizzierten Schaltung wird die Spannungsquelle (50 V) nach 0.1 Sekunden zugeschaltet Das Diagramm (unten) zeigt den zeitlichen Verlauf der Stromstärken in den drei Widerstandselementen. Das erste Element (R₁) hat einen Widerstand von 2500 Ω.

1. Berechnen Sie Spannung über dem Widerstand 1 und die darin umgesetzte Leistung unmittelbar nach dem Zuschalten der Spannungsquelle.
2. Wie viel Ladung speichert der Kondensator mit der Kapazität C zum Zeitpunkt 1.00 Sekunde?
3. Wie gross ist der Widerstand 2 und welche Leistung setzt er zum Zei'tpunkt 1.00 Sekunden um?
4. Wie gross ist die Kapazität des Kondensators?

Aufgabe 3

Das nebenstehend skizziert Diagramm zeigt die Beschleunigung eines Zuges (Masse 120 t) in Funktion der Zeit. Die Widerstandskraft auf den Zug berechnet sich nach der Formel

F_W = 2 kN + 9.8 Ns²/m2*v²

1. Wie schnell fährt dieser Zug nach 50 s?
2. Skizzieren sie das Geschwindigkeits-Zeit-Diagramm und ermitteln Sie die in diesen 50 s zurückgelegte Strecke.
3. Wie stark ist der Impulsstrom, der zum Zeitpunkt 20 s von der Erde in den Zug fliesst (Haftreibungskraft)?
4. Wie gross ist die Leistung, die das Antriebssystem zum Zeitpunkt 20 s mindestens abgeben muss?

Aufgabe 4

Ein Hammer (Masse 400 g) schlägt mit einer Geschwindigkeit von 10 m/s gegen einen horizontal ausgerichteten Nagel (Masse 3 g). Durch diesen Schlag dringt der Nagel 2 cm in die Wand ein.

1. Wie gross ist die mittlere Kraft, mit der die Wand auf den Nagel einwirkt? Nehmen Sie bei der Antwort zu dieser Frage an, dass zwischen Hammer und Nagel keine Energie dissipiert wird.
2. Skizzieren Sie für diesen Prozess ein Flüssigkeitsbild. Wählen Sie den Zeitpunkt so, dass der Hammer auf den Nagel aufschlägt, aber immer noch schneller als der Nagel ist.
3. Skizzieren Sie das Systemdiagramm (Flowchart) für diesen Prozess. Modellieren Sie die Wechselwirkung zwischen Hammer und Nagel als lineares Feder-Dämpfer-System.
4. Schreiben Sie die notwendigen Gleichungen ins Systemdiagramm hinein.

Aufgabe 5

Ein zweistrahliges Flugzeug (Masse 120 t) fliegt mit einer konstanter Schnelligkeit von 540 km/h in ruhender Luft eine Kurve mit einem Radius von 5 km. Die beiden Triebwerke wirken mit einer Schubkraft von total 70 kN auf das Flugzeug ein (35 kN pro Triebwerk). Auf dieser Flughöhe hat die Luft eine Dichte von 0.8 kg/m³.

1. Wie stark ist das Flugzeug beschleunigt, um welchen Winkel ist die Flügelebene gegen die Horizontale geneigt und wie gross ist die Auftriebskraft auf das Flugzeug?
2. Was zeigt eine Personenwaage im Flugzeug an, wenn eine Person (Masse 75 kg) während des Kurvenflugs darauf steht? Die Waage zeigt den Wert in Kilogramm und auf 100 g genau an.
3. Wie stark ist der mittlere Massenstrom durch eines der beiden Triebwerke, wenn die Austrittgeschwindigkeit relativ zum Flugzeug 300 m/s beträgt?
4. Wie gross ist die minimale Prozessleistung eines Triebwerkes, um den Luftstrom von der Eintritts- auf die Austrittsgeschwindigkeit zu beschleunigen? Wie gross ist die Leistung der Schubkraft eines Triebwerks auf das Flugzeug?

Lösung