Kraft: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) |
||
| Zeile 8: | Zeile 8: | ||
==Beispiele== |
==Beispiele== |
||
===Klotz an einer Feder=== |
===Klotz an einer Feder=== |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | Ein Klotz hängt über |
||
| ⚫ | |||
Im linken Bild sind die Impulsströme skizziert. Der ''z''-Impuls fliesst aus dem Gravitationsfeld in den Klotz hinein (Impulsquelle). Weil ein Teil im Körper bleibt, nimmt dessen Impuls zu, wobei der Impulsinhalt des Klotzes im Moment kleiner, grösser oder gleich Null sein kann. Der Rest des gravitativ zufliessenden Impulses geht direkt durch die Feder nach oben weg. Im Ring verzweigt sich der ''z''-Impulsstrom und teilt sich auf beide Seile auf. Weil in den Seilen der ''z''-Impuls seitwärts transportiert wird, induziert er einen ''x''-Impulsstrom, der von rechts nach links strömt. Die Impulserhaltung und das spezielle Systemverhalten der [[Seil |
Im linken Bild sind die Impulsströme skizziert. Der ''z''-Impuls fliesst aus dem Gravitationsfeld in den Klotz hinein (Impulsquelle). Weil ein Teil im Körper bleibt, nimmt dessen Impuls zu, wobei der Impulsinhalt des Klotzes im Moment kleiner, grösser oder gleich Null sein kann. Der Rest des gravitativ zufliessenden Impulses geht direkt durch die Feder nach oben weg. Im Ring verzweigt sich der ''z''-Impulsstrom und teilt sich auf beide Seile auf. Weil in den Seilen der ''z''-Impuls seitwärts transportiert wird, induziert er einen ''x''-Impulsstrom, der von rechts nach links strömt. Die Impulserhaltung und das spezielle Systemverhalten der [[Seil|Seile]] legen die Stärken der einzelnen Impulsströme fest. |
||
Rechts sind die Schnittbilder für Klotz, Feder und |
Rechts sind die Schnittbilder für Klotz, Feder und Ring gezeichnet. Die Summe über alle Kräfte eines Systems ergibt dessen Impulsänderungsrate. Es dürfen also nur gleichfarbige Kräfte miteinander verrechnet werden (gleichfarbige Kräfte gehören zum gleichen Vektorraum). Zwei verschiedenfarbige Kraftpfeile mit gleichem Namen bilden ein [[Wechselwirkungsprinzip|Wechselwirkungspaar]] (Actio gleich Reactio). |
||
Kraftpfeile sind graphische Darstellungen der Impulsstromstärken. Im unteren Teil der Anordung entspricht jeder Kraftpfeil einer Stromstärke des ''z''-Impulses. Beim Ring muss man zwei Kräfte (''F<sub>2</sub>'' und ''F<sub>3</sub>'') zuerst in eine ''x''- und eine ''z''-Komponente zerlegen. Die beiden Komponenten entsprechen dann den Stromstärken der beiden Impuls"sorten". |
Kraftpfeile sind graphische Darstellungen der Impulsstromstärken. Im unteren Teil der Anordung entspricht jeder Kraftpfeil einer Stromstärke des ''z''-Impulses. Beim Ring muss man zwei Kräfte (''F<sub>2</sub>'' und ''F<sub>3</sub>'') zuerst in eine ''x''- und eine ''z''-Komponente zerlegen. Die beiden Komponenten entsprechen dann den Stromstärken der beiden Impuls"sorten". |
||
Wenn man sich auf die Gleichgewichtssituation beschränkt, in die Feder und in die beiden Seile je einen Kraftpfeil einzeichnet und dann zeigt, dass die Vektorsumme der drei Pfeile Null ergibt, scheint der Kraftbegriff konkreter als das Impulsstrombild zu sein. Nur ist man dann unprofessionell vorgegangen (keine sauber definierten Schnittbilder), hat implizit eine undeklarierte Eigenschaft der Seile verwendet (der Kraftpfeil zeigt immer in Seilrichtung) und verkennt, dass eine Kraft keine reale Grösse sein kann. Eine Stromstärke ist nur ein momentanes Mass für die Stärke eines Transportes durch eine willkürlich festgelegte '''Referenzfläche'''. |
|||
===Zimmermannssäge=== |
===Zimmermannssäge=== |
||
Version vom 17. Oktober 2006, 12:22 Uhr
Kraft und Impuls
Eine Kraft ist eine Impulsstromstärke oder eine Impulsquellenstärke bezüglich eines Systems. Impulsströme treten über die Oberfläche, Impulsquellen koppeln an das Gravitationsfeld oder das elektromagnetische Feld. Die Kraft wird in Newton (N; 1 Ns = 1 kgm/s2) gemessen. Als Formelzeichen verwenden wir F oder (Fx, Fy, Fz).
Zwischen den Stromstärken der drei Impulskomponenten und den entsprechenden drei Komponenten der Kraft besteht folgender Zusammenhang: ein zufliessender Impulsstrom ergibt eine positive Kraftkomponente, ein abfliessender Impulsstrom ergibt eine negative Kraftkomponente. Der Kraftpfeil markiert also mit seinen drei Komponenten die Stärken der entsprechenden Impulsströme. Mit dieser Zuweisung ist das Wechselwirkungsprinzip abschliessen erklärt: die Stärke eines Impulsstromes ist bezüglich der beiden beteiligten Systeme entgegengesetzt gleich gross.
Beispiele
Klotz an einer Feder
Ein Klotz hängt über Feder und Ring an zwei Seilen. Wir treffen nun die Annahme, dass nur der Klotz eine Masse besitze. Der Klotz befinde sich oberhalb der Gleichgewichtslage; die Feder ist also nur wenig gespannt. Im Moment kann sich der Klotz nach oben, nach unten oder gar nicht bewegen.
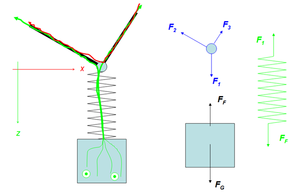
Im linken Bild sind die Impulsströme skizziert. Der z-Impuls fliesst aus dem Gravitationsfeld in den Klotz hinein (Impulsquelle). Weil ein Teil im Körper bleibt, nimmt dessen Impuls zu, wobei der Impulsinhalt des Klotzes im Moment kleiner, grösser oder gleich Null sein kann. Der Rest des gravitativ zufliessenden Impulses geht direkt durch die Feder nach oben weg. Im Ring verzweigt sich der z-Impulsstrom und teilt sich auf beide Seile auf. Weil in den Seilen der z-Impuls seitwärts transportiert wird, induziert er einen x-Impulsstrom, der von rechts nach links strömt. Die Impulserhaltung und das spezielle Systemverhalten der Seile legen die Stärken der einzelnen Impulsströme fest.
Rechts sind die Schnittbilder für Klotz, Feder und Ring gezeichnet. Die Summe über alle Kräfte eines Systems ergibt dessen Impulsänderungsrate. Es dürfen also nur gleichfarbige Kräfte miteinander verrechnet werden (gleichfarbige Kräfte gehören zum gleichen Vektorraum). Zwei verschiedenfarbige Kraftpfeile mit gleichem Namen bilden ein Wechselwirkungspaar (Actio gleich Reactio).
Kraftpfeile sind graphische Darstellungen der Impulsstromstärken. Im unteren Teil der Anordung entspricht jeder Kraftpfeil einer Stromstärke des z-Impulses. Beim Ring muss man zwei Kräfte (F2 und F3) zuerst in eine x- und eine z-Komponente zerlegen. Die beiden Komponenten entsprechen dann den Stromstärken der beiden Impuls"sorten".
Wenn man sich auf die Gleichgewichtssituation beschränkt, in die Feder und in die beiden Seile je einen Kraftpfeil einzeichnet und dann zeigt, dass die Vektorsumme der drei Pfeile Null ergibt, scheint der Kraftbegriff konkreter als das Impulsstrombild zu sein. Nur ist man dann unprofessionell vorgegangen (keine sauber definierten Schnittbilder), hat implizit eine undeklarierte Eigenschaft der Seile verwendet (der Kraftpfeil zeigt immer in Seilrichtung) und verkennt, dass eine Kraft keine reale Grösse sein kann. Eine Stromstärke ist nur ein momentanes Mass für die Stärke eines Transportes durch eine willkürlich festgelegte Referenzfläche.