Magnusrolle: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
==Theorie== |
==Theorie== |
||
Auf den rotierenden Zylinder wirken drei Kräfte ein, die Gewichtskraft (Impulsaustausch über das Gravitationsfeld), der Luftwiderstand und die Magnuskraft. Luftwiderstand und Magnuskraft gehören ursächlich zusammen. Der Luftwiderstand ist der dissipativ wirkende Anteil des |
Auf den rotierenden Zylinder wirken drei [[Kraft|Kräfte]] ein, die Gewichtskraft (Impulsaustausch über das [[Gravitationsfeld]]), der Luftwiderstand und die [[Magnus-Effekt]] Magnuskraft. Luftwiderstand und Magnuskraft gehören ursächlich zusammen. Der Luftwiderstand ist der dissipativ wirkende Anteil des [[Impuls]]austausches mit der Luft; der [[Luftwiderstand]] wirkt folglich gegen die momentane Anströmmgeschwindigkeit. Die Magnuskraft ist die normal zur Geschwindigkeit stehende Komponente der Luftkraft. |
||
Anhand einer einfachen Energieüberlegung kann für den [[Luftwiderstand]] eine Näherungsformel abgeleitet werden. Um den Einfluss der Körperform (Zylinder, Kugel, Halbkugel) zu beschreiben, wird ein zusätzlicher Formfaktor (Widerstandsbeiwert ''c<sub>W</sub>'') eingeführt. Widerstandswert und Querschnittsfläche dürfen zur effektiven Fläche zusammengefasst werden |
Anhand einer einfachen Energieüberlegung kann für den [[Luftwiderstand]] eine Näherungsformel abgeleitet werden. Um den Einfluss der Körperform (Zylinder, Kugel, Halbkugel) zu beschreiben, wird ein zusätzlicher Formfaktor (Widerstandsbeiwert ''c<sub>W</sub>'') eingeführt. Widerstandswert und Querschnittsfläche dürfen zur effektiven Fläche zusammengefasst werden |
||
| Zeile 9: | Zeile 9: | ||
<math>\vec F_W = -\frac {\rho}{2} c_W A_{quer} |\vec v| \vec v = -\frac {\rho}{2} A_{eff} |\vec v| \vec v</math> |
<math>\vec F_W = -\frac {\rho}{2} c_W A_{quer} |\vec v| \vec v = -\frac {\rho}{2} A_{eff} |\vec v| \vec v</math> |
||
Die [[Magnus-Effekt]] hängt von der Winkelgeschwindigkeit des Zylinders und von der Anströmgeschwindigkeit ab. Für die speziellen Eigenheiten des Körpers wird ein zweiten Formfaktor eingeführt |
Die [[Magnus-Effekt]] hängt von der [[Winkelgeschwindigkeit]] des Zylinders und von der Anströmgeschwindigkeit ab. Für die speziellen Eigenheiten des Körpers wird ein zweiten Formfaktor eingeführt |
||
<math>\vec F_M = \rho r c_M A_{quer} (\vec \omega x \vec v)</math> |
<math>\vec F_M = \rho r c_M A_{quer} (\vec \omega x \vec v)</math> |
||
Version vom 22. Dezember 2006, 08:16 Uhr
Das Objekt
Ein Hohlzylinder aus Karton wird mit Hilfe eines aufgewickelten Stoffbandes weggeschleudert und gleichzeitig in Rotation versetzt. Abhängig vom Wicklungssinn des Bandes steigt der Zylinder auf oder fliegt sehr schnell zu Boden. Mit etwas Übung bringt man den rotierenden Zylinder auf eine schleifenförmige Bahn (Looping). Diese verblüffende Bahnabweichung des rotierenden Körpers, die bei vielen Ballspielen bewusst eingesetzt wird, heisst Magnuseffekt.
Theorie
Auf den rotierenden Zylinder wirken drei Kräfte ein, die Gewichtskraft (Impulsaustausch über das Gravitationsfeld), der Luftwiderstand und die Magnus-Effekt Magnuskraft. Luftwiderstand und Magnuskraft gehören ursächlich zusammen. Der Luftwiderstand ist der dissipativ wirkende Anteil des Impulsaustausches mit der Luft; der Luftwiderstand wirkt folglich gegen die momentane Anströmmgeschwindigkeit. Die Magnuskraft ist die normal zur Geschwindigkeit stehende Komponente der Luftkraft.
Anhand einer einfachen Energieüberlegung kann für den Luftwiderstand eine Näherungsformel abgeleitet werden. Um den Einfluss der Körperform (Zylinder, Kugel, Halbkugel) zu beschreiben, wird ein zusätzlicher Formfaktor (Widerstandsbeiwert cW) eingeführt. Widerstandswert und Querschnittsfläche dürfen zur effektiven Fläche zusammengefasst werden
[math]\vec F_W = -\frac {\rho}{2} c_W A_{quer} |\vec v| \vec v = -\frac {\rho}{2} A_{eff} |\vec v| \vec v[/math]
Die Magnus-Effekt hängt von der Winkelgeschwindigkeit des Zylinders und von der Anströmgeschwindigkeit ab. Für die speziellen Eigenheiten des Körpers wird ein zweiten Formfaktor eingeführt
[math]\vec F_M = \rho r c_M A_{quer} (\vec \omega x \vec v)[/math]
Die Luft bremst über die mitgerissene Grenzschicht die Rotation des Zylinders. Mangels exakter Theorie machen wir für das auf den Zylinder einwirkende Drehmoment eine plausible Abschätzung. Die Unsicherheiten bezüglich der Wirkung steckt im dritten Formfaktor (cR)
[math]M = \frac {\rho}{2} r^3 c_R A_{quer} \omega^2[/math]
Simulationsmodell
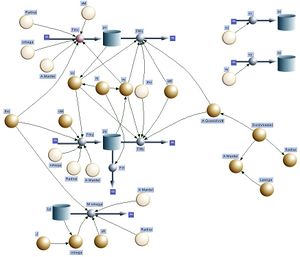
Das Grundgerüst des Simulationsmodells wird von drei Bilanzgleichungen gebildet, den Impulsbilanzen für die zwei Richtungen sowie der zugehörigen Drehimpulsbilanz. Die konstitutiven Gesezte sind entweder grundlegend (Masse und Massenträgheitsmoment als Kapazitäten) oder weiter oben schon diskutiert worden. Beim Start ist die Geschwindigkeit horizontal gerichtet und die Winkelgeschwindigkeit ist gleich Geschwindigkeitsbetrag dividiert durch Zylinderradius.
Simulation
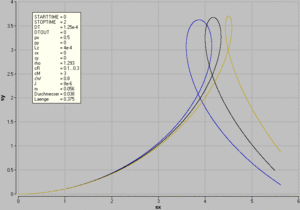
Der Widerstandsbeiwert kann einem Tabellenbuch entnommen werden. Die beiden andern Formfaktoren sind anhand der experimentellen Erfahrung geschätz worden. Die Graphik zeigt eine Parameterstudie für den Formfaktor des reibenden Drehmoments.