Lösung zu Dynamik des Bugrades: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Bezüglich des gezeichneten Koordinatensystems fliesst sehr wahrscheinlich ''x''-[[Impuls]] aus dem Rest des Flugzeuges zu und geht zusammen mit dem ''x''-Impuls, den das Rad abgibt, an die Unterlage weg. ''y''-Impulses fliesst vom Gravitationsfeld her zu und vereinigt sich im Rad mit dem über die Achse zugeführten Teil. Weil das Rad in ''y''-Richtung keinen Impuls speichern kann, muss der ganze Zufluss direkt an die Erde abfliessen. Der seitwärts |
Bezüglich des gezeichneten Koordinatensystems fliesst sehr wahrscheinlich ''x''-[[Impuls]] aus dem Rest des Flugzeuges zu und geht zusammen mit dem ''x''-Impuls, den das Rad abgibt, an die Unterlage weg. ''y''-Impulses fliesst vom Gravitationsfeld her zu und vereinigt sich im Rad mit dem über die Achse zugeführten Teil. Weil das Rad in ''y''-Richtung keinen Impuls speichern kann, muss der ganze Zufluss direkt an die Erde abfliessen. Der seitwärts strömende ''x''-Impuls erzeugt Quellen des ''z''-[[Drehimpuls]]es (Achse normal zur Skizze, nach hinten orientiert). |
||
[[Bild:Bugrad_Kraefte.png|thumb|Kräfte auf das Bugrad]] |
[[Bild:Bugrad_Kraefte.png|thumb|Kräfte auf das Bugrad]] |
||
Die Kraftskizze ergibt sich aus den oben beschriebenen Impulsströmen. Die Stärken der über das Lager von der Achse her zufliessenden ''x''- und ''y''-Impulsströme sind hier zu einem einzigen Kraftpfeil zusammengefasst. Oft lässt man die Zerlegung stehen, weil man die Bilanzgleichungen schlussendlich |
Die Kraftskizze ergibt sich aus den oben beschriebenen Impulsströmen. Die Stärken der über das Lager von der Achse her zufliessenden ''x''- und ''y''-Impulsströme sind hier zu einem einzigen Kraftpfeil zusammengefasst worden. Oft lässt man die Zerlegung einer Kraft in ihre drei Komponenten stehen, weil man die Bilanzgleichungen schlussendlich auch komponentenweise formulieren muss. |
||
In einem zweiten Schritt stellt man die drei Bilanzgleichungen auf und verwendet für den Inhalt direkt die [[kapazitives Gesetz|kapazitiven Gesetze]] |
In einem zweiten Schritt stellt man die drei Bilanzgleichungen auf und verwendet für den Inhalt direkt die [[kapazitives Gesetz|kapazitiven Gesetze]] |
||
| Zeile 8: | Zeile 8: | ||
''x''-Impuls: <math>F_{Ax} - F_R = m \dot v_x</math> |
''x''-Impuls: <math>F_{Ax} - F_R = m \dot v_x</math> |
||
''y''-Impuls: <math>F_{Ay} + m g |
''y''-Impuls: <math>F_{Ay} + m g - F_N = 0</math> |
||
''z''-Drehimpuls: <math>F_N |
''z''-Drehimpuls: <math>F_N R = J \dot \omega</math> |
||
Man kann diese Aufgabe natürlich ohne Kenntnis der [[Physik der dynamischen Systeme]] lösen. Dann zeichnet man die Wirkungen aufgrund der Erfahrung ein, dass an jeder Schnittfläche maximal eine Kraft (drei Komponenten) und ein Drehmoment (drei Komponenten) einwirken kann. |
|||
Zu den einzelnen Fragen: |
|||
#Das [[Freischneiden|Schnittbild]] enthält alle Kräfte und Drehmomente. Unbestimmte Grössen werden nach belieben eingezeichnet, aber dann mit den skizzierten Richtungen in die Bilanzgleichungen (Grundgesetze) übernommen. |
|||
#Die Grösse der Gleitreibungskraft ergibt sich aus der Drehimpulsbilanz <math>F_R = \frac {J \dot \omega}{R} </math> = 100 N |
|||
#Die Grösse der Normalkraft berechnet sich mit Hilfe des Gesetzes zur Gleitreibung (Coulombsche Reibung) <math>F_N = \frac {F_R}{\mu}</math> = 167 N. |
|||
#Die beiden Komponenten der Achsenkraft ergeben sich aus den beiden Impulsbilanzen: 260 N in ''x''-Richtung und 951 N in ''y''-Richtung. Die Achsenkraft hat somit einen Betrag von 986 N. |
|||
'''[[Dynamik des Bugrades|Aufgabe]]''' |
|||
Version vom 24. April 2007, 14:03 Uhr
Bezüglich des gezeichneten Koordinatensystems fliesst sehr wahrscheinlich x-Impuls aus dem Rest des Flugzeuges zu und geht zusammen mit dem x-Impuls, den das Rad abgibt, an die Unterlage weg. y-Impulses fliesst vom Gravitationsfeld her zu und vereinigt sich im Rad mit dem über die Achse zugeführten Teil. Weil das Rad in y-Richtung keinen Impuls speichern kann, muss der ganze Zufluss direkt an die Erde abfliessen. Der seitwärts strömende x-Impuls erzeugt Quellen des z-Drehimpulses (Achse normal zur Skizze, nach hinten orientiert).
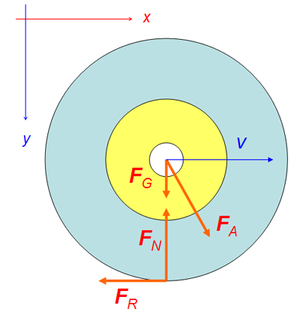
Die Kraftskizze ergibt sich aus den oben beschriebenen Impulsströmen. Die Stärken der über das Lager von der Achse her zufliessenden x- und y-Impulsströme sind hier zu einem einzigen Kraftpfeil zusammengefasst worden. Oft lässt man die Zerlegung einer Kraft in ihre drei Komponenten stehen, weil man die Bilanzgleichungen schlussendlich auch komponentenweise formulieren muss.
In einem zweiten Schritt stellt man die drei Bilanzgleichungen auf und verwendet für den Inhalt direkt die kapazitiven Gesetze
x-Impuls: [math]F_{Ax} - F_R = m \dot v_x[/math]
y-Impuls: [math]F_{Ay} + m g - F_N = 0[/math]
z-Drehimpuls: [math]F_N R = J \dot \omega[/math]
Man kann diese Aufgabe natürlich ohne Kenntnis der Physik der dynamischen Systeme lösen. Dann zeichnet man die Wirkungen aufgrund der Erfahrung ein, dass an jeder Schnittfläche maximal eine Kraft (drei Komponenten) und ein Drehmoment (drei Komponenten) einwirken kann.
Zu den einzelnen Fragen:
- Das Schnittbild enthält alle Kräfte und Drehmomente. Unbestimmte Grössen werden nach belieben eingezeichnet, aber dann mit den skizzierten Richtungen in die Bilanzgleichungen (Grundgesetze) übernommen.
- Die Grösse der Gleitreibungskraft ergibt sich aus der Drehimpulsbilanz [math]F_R = \frac {J \dot \omega}{R} [/math] = 100 N
- Die Grösse der Normalkraft berechnet sich mit Hilfe des Gesetzes zur Gleitreibung (Coulombsche Reibung) [math]F_N = \frac {F_R}{\mu}[/math] = 167 N.
- Die beiden Komponenten der Achsenkraft ergeben sich aus den beiden Impulsbilanzen: 260 N in x-Richtung und 951 N in y-Richtung. Die Achsenkraft hat somit einen Betrag von 986 N.