Loch im Topf

In den Boden einer Büchse (Querschnitt A = ) ist ein Kreisrundes Loch (Durchmesser d = ) gebohrt worden. Wie verändert sich die Füllhöhe mit in der Zeit, falls die Büchse anfänglich 10 cm hoch mit Wasser gefüllt worden ist?

Theorie

Schon Evangelista Torricelli konnte zeigen, dass das ausfliessende Wasser die gleiche Geschwindigkeit aufweist, wie ein Körper, der von der Wasseroberfläche um die gleiche Höhe hinunter gefallen ist. Somit gilt

[math]v=\sqrt{2gh}[/math]

wobei h für die Füllhöhe steht und mit g die Gravitationsfeldstärke gemeint ist.

Die Stärke des ausfliessenden Volumenstromes ist gleich Querschnitt des Wasserstrahls mal Austströmgeschwindigkeit

[math]I_V=A_S v[/math]

Man beachte, dass der Strahlquerschnitt oft kleiner als die Bohrung ist. Bei einem scharfkantigen Loch macht die Einschnürung etwa 40 % aus. Der Querschnitt des Strahls beträgt dann nur noch etwa 60 % des Querschnitts des Lochs.

Modell

Systemdiagramm

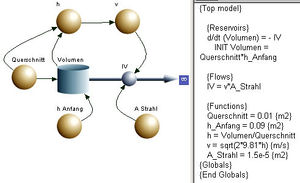
Die Volumenbilanz bildet den Kern des Modells. Folglich zeichnet man im Systemdiagramm (flowchart) einen Topf (reservoir) und hängt eine Leitung (flow) mit Bezugsrichtung nach aussen an. Dividiert man das gespeicherte Volumen durch den Querschnitt der Büchse oder des Topfs, erhält man die aktuelle Füllhöhe. Umgekehrt kann das Anfangsvolumen als Querschnitt mal anfängliche Füllhöhe geschrieben werden. Mit Hilfe des Ausflussgesetzes von Torricelli lässt sich die Ausflussgeschwindigkeit berechnen. Die Stärke des Volumenstroms ist dann gleich Ausflussgeschwindigkeit mal Querschnitt des Freistrahls.

Damit dieses Modell berechnet werden kann, müssen alle Parameter gesetzt werden. Nimmt man eine Blechbüchse für Elisenlebkuchen und bohrt ein Loch mit einem Durchmesser von 5 mm hinein, gelten etwa folgende Werte

• Querschnitt der Büchse 0.01 m²
• Querschnitt des Freistrahls 1.5 10^-5 m²
• Füllhöhe 0.09 m

Simulation

Füllhöhe und Volumenstrom

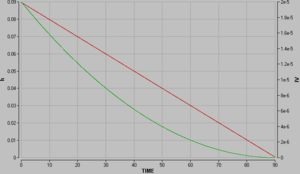
Dieses Modell ist problemlos zu simulieren, solange der Topf noch nicht leer ist. Weil zur Berechnung der Ausflussgeschwindigkeit die Wurzel aus der doppelten Gravitationsfeldstärke mal die Füllhöhe (Torricelli) gezogen werden muss, tauchen numerische Probleme auf, sobald der Topf leer wird. Ist der Topf praktisch leer, kann es passieren, dass im nächsten Rechenschritt die Volumenstromstärke mal der Zeitschritt einen grösseren Wert liefert, als an Volumen noch im Topf drin ist. Dann wird die Füllhöhe negativ und die Wurzel lässt sich im nächsten Rechenschritt nicht mehr ziehen. Folglich reagiert das Simulationsprogramm mit einer Fehlermeldung. Die hier gesetzten Parameter (Querschnitt der Büchse und des Freistrahls, Anfangshöhe) liefern eine Ausflusszeit von gut 90 Sekunden. Also darf die Zeit (stoptime) auf 90 gesetzt werden.

Die Simulation zeigt ein unerwartetes Ergebnis. Obwohl das Ausflussgesetz von Torricelli nicht linear ist, nimmt die Stärke des Volumenstromes und damit auch die Ausflussgeschwindigkeit linear mit der Zeit ab. Die Füllhöhe und damit auch der Inhalt der Büchse gehen deshalb quadratisch in der Zeit zurück. Schon nach 45 Sekunden ist die Büchse nur noch zu einem Viertel gefüllt.