Sprung aus Stratosphäre

Der 64-jährige Michel Fournier will aus 40'000 Meter Höhe abspringen. Eine an einem Heliumballon hängende Druckkabine soll ihn in drei Stunden auf diese Höhe bringen. Fournier hat sein Haus, seine Wertsachen und seine Pension in dieses 19 Millionen Franken teure Unternehmen investiert. Nachfolgend das systemdynamische Modell des Absprunges.

Modell

Systemdiagramm der Sprungdynamik

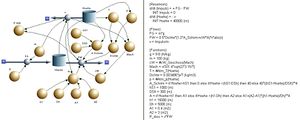
Die Impulsbilanz mit der Gewichtskraft als Impulsquelle und dem Luftwiderstand als Impulsabfluss bildet den Kern des Modells. Weil die positive Richtung nach unten orientiert ist, die Höhe aber positiv sein soll, wird die negative Geschwindigkeit (Impuls/Masse) zur Höhe aufintegriert. In die Berechnung des Luftwiderstands gehen eine von der Höhe abhängige Dichte, der c_W-Wert als Funktion der Machzahl und eine variable Fläche ein. Die Fläche ist anfänglich klein, weil Fournier versuchen wird, der Luft bis zum Erreichen der Maximalgeschwindigkeit möglichst wenig Widerstand entgegen zu setzen. Danach will er sich breit machen, damit der Fall möglichst lange dauert. Auf den letzten tausend Metern Höhe wirkt dann noch ein Fallschirm. Der Luftdruck und die zugehörige Temperatur, die in die Dichte bzw. die Machzahl einfliessen, entsprechen der ICAO-Standardatmosphäre. Der Zusammenhang zwischen Widerstandsbeiwert und Machzahl ist der Ballistik entnommen. Weil Projektile eher kleine Widerstandsbeiwerte aufweisen, müssen hier etwas grosse Querschnitte eingesetzt werden.

Simulation

Höhen-Geschwindigkeitsprofil

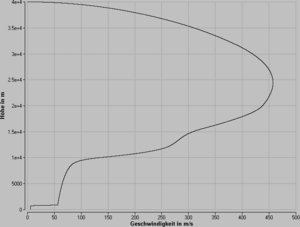
Die Graphik zeigt das Höhen-Geschwindigkeitsprofil des Sprungs. Fournier wird Mach 1 auf einer Höhe von etwa 35 km erreichen. Seine Körperhaltung wird infolge der geringen Dichte der Luft wenig Einfluss auf diese Geschwindigkeit haben. Die Maximalgeschwindigkeit wird etwa 1.5 Mach betragen, wenn es Fournier gelingt, den Körper in senkrechter Lage gestreckt zu halten. Der weitere Verlauf der Bewegung (Fallzeit und Geschwindigkeit) hängt dann ziemlich stark vom Verhalten Fourniers ab.