Lösung zu Widerstand einer Glühbirne: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 19: | Zeile 19: | ||
|} |
|} |
||
#Die Stromstärke ist gleich Spannung durch Widerstand <math>I=\frac{U}{R}</math> = 5. |
#Die Stromstärke ist gleich Spannung durch Widerstand <br><math>I=\frac{U}{R}=\frac{12 V}{2.35 \Omega }</math> = 5.11 A. |
||
#Die Leistung ist gleich Spannung über dem Draht mal Stromstärke durch den Draht <math>P=UI=\frac{U^2}{R}</math> = 16.1 W, 46.5 W, 78.4 W. |
#Die Leistung ist gleich Spannung über dem Draht mal Stromstärke durch den Draht <br><math>P=UI=\frac{U^2}{R}</math> = 16.1 W, 46.5 W, 78.4 W. |
||
#Der kleinstmögliche Widerstand von etwa 0.15 Ω entspricht dem Kaltwiderstand R<sub>20</sub>. Nun verwenden wir für den Widerstand die quadratische Gleichung mit der Temperaturerhöhung. Diese lösen wir nach der Temperaturerhöhung auf und erhalten dann 3 Werte für die Temperaturerhöhung: ''Δ T'' = 1641°C, 2156°C und 2430°C. Die gesuchten Drahttemperaturen betragen also 1661°C, 2176°C und 2450°C. |
#Der kleinstmögliche Widerstand von etwa 0.15 Ω entspricht dem Kaltwiderstand R<sub>20</sub>. Nun verwenden wir für den Widerstand die quadratische Gleichung mit der Temperaturerhöhung. Diese lösen wir nach der Temperaturerhöhung auf und erhalten dann 3 Werte für die Temperaturerhöhung: ''Δ T'' = 1641°C, 2156°C und 2430°C. Die gesuchten Drahttemperaturen betragen also 1661°C, 2176°C und 2450°C. |
||
#Das Diagramm zeigt die 3 Werte nicht auf einer Geraden sondern auf einer leicht gekrümmten Kurve. Zu dieser Abweichung können verschiedene Effekte beitragen: Wärmeverluste durch Wärmeleitung über die Anschlussdrähte, Spannungsverlust bei den Anschlussdrähten, Konvektionsverluste an das Gas im Lampenkolben, ... |
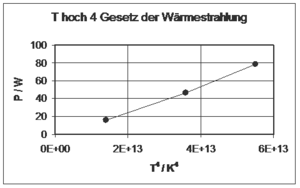
#Das Diagramm P gegen T<sup>4</sup> zeigt die 3 Werte nicht auf einer Geraden sondern auf einer leicht gekrümmten Kurve. Zu dieser Abweichung können verschiedene Effekte beitragen: Wärmeverluste durch Wärmeleitung über die Anschlussdrähte, Spannungsverlust bei den Anschlussdrähten, Konvektionsverluste an das Gas im Lampenkolben, ... |
||
[[Bild:Thoch4_Gesetz.png|thumb|Glühbirne: Leistung gegen T<sup>4</sup>]] |
[[Bild:Thoch4_Gesetz.png|thumb|Glühbirne: Leistung gegen T<sup>4</sup>]] |
||
Zum Lösen von quadratischen Gleichungen: Zuerst bringt man die gegebene Gleichung in Normalform: <math>ax^2+bx+c=0</math>. Dann berechnet man die 2 möglichen Lösungen mit folgender Formel: <math>x_{1,2} = (-b \pm \sqrt {b^2-4ac})/(2a)</math> und wählt dann daraus die physikalisch sinnvolle Lösung aus (hier ist es die positive Lösung, weil eine negative Temperaturerhöhung hier keinen Sinn ergibt). |
Zum Lösen von quadratischen Gleichungen: Zuerst bringt man die gegebene Gleichung in Normalform: <math>ax^2+bx+c=0</math>. Dann berechnet man die 2 möglichen Lösungen mit folgender Formel: <math>x_{1,2} = (-b \pm \sqrt {b^2-4ac})/(2a)</math> und wählt dann daraus die physikalisch sinnvolle Lösung aus (hier ist es die positive Lösung, weil eine negative Temperaturerhöhung hier keinen Sinn ergibt). Oder einfacher mit einem Taschenrechner, der mit der Solve-Funktion quadratische Gleichungen auflöst. |
||
Version vom 15. Juli 2009, 14:02 Uhr
Die zu den Spannungswerten benötigten Widerstandswerte liest man aus dem Diagramm R-U-Charakteristik ab:
| 0 V | 0.15 Ω |
| 5 V | 1.55 Ω |
| 10 V | 2.15 Ω |
| 12 V | 2.35 Ω |
| 14 V | 2.50 Ω |
- Die Stromstärke ist gleich Spannung durch Widerstand
[math]I=\frac{U}{R}=\frac{12 V}{2.35 \Omega }[/math] = 5.11 A. - Die Leistung ist gleich Spannung über dem Draht mal Stromstärke durch den Draht
[math]P=UI=\frac{U^2}{R}[/math] = 16.1 W, 46.5 W, 78.4 W. - Der kleinstmögliche Widerstand von etwa 0.15 Ω entspricht dem Kaltwiderstand R20. Nun verwenden wir für den Widerstand die quadratische Gleichung mit der Temperaturerhöhung. Diese lösen wir nach der Temperaturerhöhung auf und erhalten dann 3 Werte für die Temperaturerhöhung: Δ T = 1641°C, 2156°C und 2430°C. Die gesuchten Drahttemperaturen betragen also 1661°C, 2176°C und 2450°C.
- Das Diagramm P gegen T4 zeigt die 3 Werte nicht auf einer Geraden sondern auf einer leicht gekrümmten Kurve. Zu dieser Abweichung können verschiedene Effekte beitragen: Wärmeverluste durch Wärmeleitung über die Anschlussdrähte, Spannungsverlust bei den Anschlussdrähten, Konvektionsverluste an das Gas im Lampenkolben, ...
Zum Lösen von quadratischen Gleichungen: Zuerst bringt man die gegebene Gleichung in Normalform: [math]ax^2+bx+c=0[/math]. Dann berechnet man die 2 möglichen Lösungen mit folgender Formel: [math]x_{1,2} = (-b \pm \sqrt {b^2-4ac})/(2a)[/math] und wählt dann daraus die physikalisch sinnvolle Lösung aus (hier ist es die positive Lösung, weil eine negative Temperaturerhöhung hier keinen Sinn ergibt). Oder einfacher mit einem Taschenrechner, der mit der Solve-Funktion quadratische Gleichungen auflöst.