Lösung zu Kreisprozess dreiteilig: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
#Im ''T-S-''Diagramm verläuft die isochore Zustandsänderung exponentiell, die isentrope vertikal und die isotherme horizontal. Im ''p-V-''Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf der <math>pV^k=p_0V_0^k</math> - Kurve nach rechts unten und auf einer Hyperbel wieder nach links oben. Im ''T-S-''Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. Im ''p-V-''Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit. |
#Im ''T-S-''Diagramm verläuft die isochore Zustandsänderung exponentiell, die isentrope vertikal und die isotherme horizontal. Im ''p-V-''Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf der <math>pV^k=p_0V_0^k</math> - Kurve nach rechts unten und auf einer Hyperbel wieder nach links oben. Im ''T-S-''Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. Im ''p-V-''Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit. |
||
#Die [[innere Energie]] eines idealen Gases hängt nur von der Temperatur ab. Im ersten Teilprozess (isochor) nimmt die innere Energie um <math>\Delta W=n\hat c_V\Delta T=\frac 3 2 nR\Delta T</math> = 187 kJ zu. Um genau diesen Betrag nimmt die innere Energie im zweiten, isentropen Prozess wieder ab. |
#Die [[innere Energie]] eines idealen Gases hängt nur von der Temperatur ab. Im ersten Teilprozess (isochor) nimmt die innere Energie um <math>\Delta W=n\hat c_V\Delta T=\frac 3 2 nR\Delta T</math> = 1.5 * 50 mol * 8.31 J/K/mol * 300 K = 187 kJ zu. Um genau diesen Betrag nimmt die innere Energie im zweiten, isentropen Prozess wieder ab, weil das Gas wieder auf die Anfangstemperatur zurückgebracht wird. Im 3. Teilprozess ändert sich die innere Energie nicht mehr, weil die Temperatur konstant bleibt. |
||
#Im ersten |
#Im ersten Teilprozess nimmt die Entropie um <math>\Delta S=n\hat c_V\ln{\frac{T_2}{T_1}}=\frac 3 2 nR\ln{\frac{T_2}{T_1}}</math> = 1.5 * 50 mol * 8.31 J/K/mol * ln(500 K / 200 K) = 571 J/K zu. Im zweiten, isentropen Teilprozess bleibt die Entropie konstant. Und im dritten, isothermen Teilprozess, der das Gas wieder auf die Anfangstemperatur zurückbringt, nimmt sie um denselben Betrag wieder ab wie im ersten Teilprozess. |
||
#Im isentropen Teilprozess ist die mechanisch abgeführten Energie gleich der Änderung der inneren Energie. Folglich ist die Arbeit gleich -187 kJ. Weil sich im dritten Teilprozess die innere Energie nicht ändert, ist die thermisch abgegebene Energie gleich der mechanisch zugeführten. Die thermisch abgeführte Energie ist gleich abgeführte Entropie mal herrschende Temperatur, also gleich -571 J/K * 200 K = -114 kJ. Die Kompressionsarbeit beträgt demnach 114 kJ. Durch Addition der beiden Arbeiten erhält man für den ganzen Zyklus eine mechanisch abgeführte Energie von -73 kJ. |
#Im isentropen Teilprozess ist die mechanisch abgeführten Energie gleich der Änderung der inneren Energie. Folglich ist die Arbeit gleich -187 kJ. Weil sich im dritten Teilprozess die innere Energie nicht ändert, ist die thermisch abgegebene Energie gleich der mechanisch zugeführten. Die thermisch abgeführte Energie ist gleich abgeführte Entropie mal herrschende Temperatur, also gleich -571 J/K * 200 K = -114 kJ. Die Kompressionsarbeit beträgt demnach 114 kJ. Durch Addition der beiden Arbeiten erhält man für den ganzen Zyklus eine mechanisch abgeführte Energie von -73 kJ. |
||
Version vom 10. April 2010, 16:42 Uhr
-
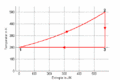
T-S-Diagramm
-
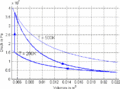
p-V-Diagramm
- Im T-S-Diagramm verläuft die isochore Zustandsänderung exponentiell, die isentrope vertikal und die isotherme horizontal. Im p-V-Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf der [math]pV^k=p_0V_0^k[/math] - Kurve nach rechts unten und auf einer Hyperbel wieder nach links oben. Im T-S-Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. Im p-V-Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit.
- Die innere Energie eines idealen Gases hängt nur von der Temperatur ab. Im ersten Teilprozess (isochor) nimmt die innere Energie um [math]\Delta W=n\hat c_V\Delta T=\frac 3 2 nR\Delta T[/math] = 1.5 * 50 mol * 8.31 J/K/mol * 300 K = 187 kJ zu. Um genau diesen Betrag nimmt die innere Energie im zweiten, isentropen Prozess wieder ab, weil das Gas wieder auf die Anfangstemperatur zurückgebracht wird. Im 3. Teilprozess ändert sich die innere Energie nicht mehr, weil die Temperatur konstant bleibt.
- Im ersten Teilprozess nimmt die Entropie um [math]\Delta S=n\hat c_V\ln{\frac{T_2}{T_1}}=\frac 3 2 nR\ln{\frac{T_2}{T_1}}[/math] = 1.5 * 50 mol * 8.31 J/K/mol * ln(500 K / 200 K) = 571 J/K zu. Im zweiten, isentropen Teilprozess bleibt die Entropie konstant. Und im dritten, isothermen Teilprozess, der das Gas wieder auf die Anfangstemperatur zurückbringt, nimmt sie um denselben Betrag wieder ab wie im ersten Teilprozess.
- Im isentropen Teilprozess ist die mechanisch abgeführten Energie gleich der Änderung der inneren Energie. Folglich ist die Arbeit gleich -187 kJ. Weil sich im dritten Teilprozess die innere Energie nicht ändert, ist die thermisch abgegebene Energie gleich der mechanisch zugeführten. Die thermisch abgeführte Energie ist gleich abgeführte Entropie mal herrschende Temperatur, also gleich -571 J/K * 200 K = -114 kJ. Die Kompressionsarbeit beträgt demnach 114 kJ. Durch Addition der beiden Arbeiten erhält man für den ganzen Zyklus eine mechanisch abgeführte Energie von -73 kJ.