Lösung zu Flugzeugstart: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 10. Februar 2010, 14:53 Uhr

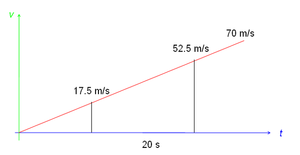
In 20 Sekunden erhöht das Flugzeug seine Geschwindigkeit um 52.5 m/s - 17.5 m/s = 35 m/s. Folglich ist die Beschleunigung gleich 35 m/s / 20 s = 1.75 m/s².
Die Strecke zwischen A und B entspricht der Fläche unter der Geschwindigkeitskurve und ist gleich mittlere Geschwindigkeit mal benötigte Zeit (Fläche des Trapezes), also gleich (52.5 m/s + 17.5 m/s) / 2 * 20 s = 700 m.
Das Flugzeug erhöht seine Geschwindigkeit in jeder Sekunde um 1.75 m/s. Bis es eine Geschwindigkeit von 70 m/s erreicht hat, benötigt es somit 70 m/s / 1.75 m/s² = 40 s.
In den fraglichen 40 s legt das Flugzeug eine Strecke (Fläche unter der v-Kurve) von 70 m/s * 40 s / 2 = 1.4 km zurück.

@@ Zeile 3: / Zeile 3: @@
 #Die Strecke zwischen A und B entspricht der Fläche unter der Geschwindigkeitskurve und ist gleich mittlere Geschwindigkeit mal benötigte Zeit (Fläche des Trapezes), also gleich (52.5 m/s + 17.5 m/s) / 2 * 20 s = 700 m.
 #Das Flugzeug erhöht seine Geschwindigkeit in jeder Sekunde um 1.75 m/s. Bis es eine Geschwindigkeit von 70 m/s erreicht hat, benötigt es somit 70 m/s / 1.75 m/s<sup>2</sup> = 40 s.
-#In den fraglichen 40 s legt das Flugzeug eine Strecke Fläche unter der v-Kurve) von 70 m/s * 40 s / 2 = 1.4 km zurück.
+#In den fraglichen 40 s legt das Flugzeug eine Strecke (Fläche unter der v-Kurve) von 70 m/s * 40 s / 2 = 1.4 km zurück.
 '''[[Flugzeugstart|Aufgabe]]'''