Lösung zu Volumen bilanzieren: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Keine Bearbeitungszusammenfassung |
(→Lösung) |
||
| Zeile 10: | Zeile 10: | ||
==Lösung== |
==Lösung== |
||
Als Volumenänderungsrate resultiert: |
|||
Als Volumenänderungsraten resultieren: |
|||
:<math>\dot V=I_{V_1}-I_{V_2}-I_{V_3}</math> |
:<math>\dot V=I_{V_1}-I_{V_2}-I_{V_3}</math> |
||
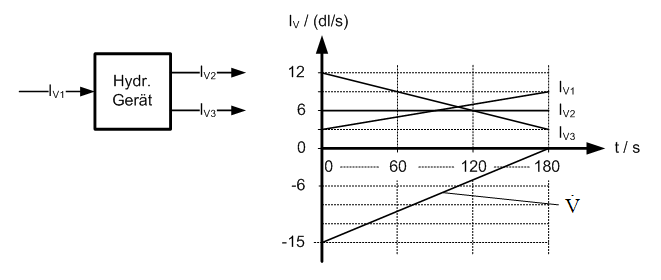
Am Anfang: 3 dl/s - 6 dl/s - 12 dl/s = -15 dl/s |
Am Anfang (t = 0 s) ist diese: 3 dl/s - 6 dl/s - 12 dl/s = -15 dl/s |
||
Am Schluss: 9 dl/s - 6 dl/s - 3 dl/s = 0 dl/s |
Am Schluss (t = 180 s): 9 dl/s - 6 dl/s - 3 dl/s = 0 dl/s |
||
Die in den Strömen geflossenen (gf) Volumina ergeben die Volumenänderung des Systems: |
Die in den Strömen geflossenen (gf) Volumina werden als Fläche unter den 3 Kurven (Dreiecke) berechnet und ergeben die Volumenänderung des Systems: |
||
:<math>\Delta V=V_{gf_1}-V_{gf_2}-V_{gf_3}</math>= (6 dl/s - 6 dl/s - 7.5 dl/s) * 180 s = -1350 dl = -135 l |
:<math>\Delta V=V_{gf_1}-V_{gf_2}-V_{gf_3}</math>= (6 dl/s - 6 dl/s - 7.5 dl/s) * 180 s = -1350 dl = -135 l |
||
Alternativ dazu kann auch die Volumenänderungs des Gerätes aus der Volumenänderungsrate berechnet werden, ebenfalls als Fläche unter der Kurve. Das ergibt ebenfalls: |
|||
1/2 * 180 s * (-1.5 l/s) = -135 l. |
|||
'''[[Volumen bilanzieren|Aufgabe]]''' |
'''[[Volumen bilanzieren|Aufgabe]]''' |
||
Version vom 27. September 2010, 13:58 Uhr
Lösungsidee
- Bei linearer Änderung der Stromstärke darf mit dem zeitlichen Mittelwert gearbeitet werden.
- Die Volumenänderung über einem Zeitabschnitt kann auf zwei Arten berechnet werden:
- entweder summiert (integriert) man die einzelnen Stromstärken über die Zeit und zählt dann alles zusammen
- oder man bestimmt zuerst die Änderungsrate und summiert (integriert) dann über die Zeit.
Volumenströme: Prinzip und Diagramm
Lösung
Als Volumenänderungsrate resultiert:
- [math]\dot V=I_{V_1}-I_{V_2}-I_{V_3}[/math]
Am Anfang (t = 0 s) ist diese: 3 dl/s - 6 dl/s - 12 dl/s = -15 dl/s
Am Schluss (t = 180 s): 9 dl/s - 6 dl/s - 3 dl/s = 0 dl/s
Die in den Strömen geflossenen (gf) Volumina werden als Fläche unter den 3 Kurven (Dreiecke) berechnet und ergeben die Volumenänderung des Systems:
- [math]\Delta V=V_{gf_1}-V_{gf_2}-V_{gf_3}[/math]= (6 dl/s - 6 dl/s - 7.5 dl/s) * 180 s = -1350 dl = -135 l
Alternativ dazu kann auch die Volumenänderungs des Gerätes aus der Volumenänderungsrate berechnet werden, ebenfalls als Fläche unter der Kurve. Das ergibt ebenfalls: 1/2 * 180 s * (-1.5 l/s) = -135 l.