Lösung zu Aviatik 2011/1

Aufgabe 1

Systemdiagramm zu Aufgabe 1

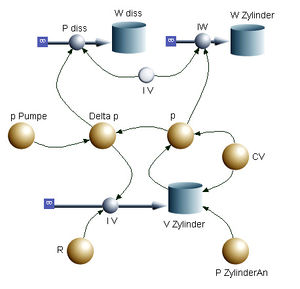
1. Siehe Systemdiagramm (flowchart)
2. Volumenstromstärke: [math]I_V=\frac{\Delta p}{R_V}[/math]; Druckdifferenz: [math]\Delta p=p_{Pumpe}-p=p_{Zylinder}[/math]; Druck im Zlinder: [math]p_{Zylinder}=\frac{V_{Zylinder}}{C_V}[/math]; Anfangsvolumen im Zylinder [math]V_{ZylinderAn}=C_V\cdot p_{ZylinderAn}[/math]
3. Siehe Systemdiagramm (flowchart)
4. Prozessleistung: [math]P=\Delta pI_V[/math]; zugeordneter Energiestrom: [math]I_W=p_{Zylinder}I_V[/math]

Aufgabe 2

1. [math]C_V=\frac{A}{\varrho g}[/math] = 8.16 10^-9 s²m⁴/kg (m³/Pa)
2. [math]W=\frac{C_V}{2}\left(\Delta p_1\right)^2[/math] = 1.57 10^-4 J; [math]W_U=2W[/math] = 3.14 10^-4 J
3. [math]C_V=\frac{\Delta V}{\Delta p}=\frac{A\Delta h}{\varrho g\Delta h+\frac{p_0}{h_0}\Delta h}=\frac{A}{\varrho g+\frac{p_0}{h_0}}[/math] = 5.4 10^-9 s²m⁴/kg (m³/Pa)
4. [math]T=2\pi\sqrt{L_{VU}C_{VU}}[/math] = 0.816 s; mit [math]C_{VU}=\frac{C_V}{2}[/math] und [math]L_{VU}=\varrho\frac{l}{A}[/math] = 6.25 10⁶ kg/m⁴

Aufgabe 3

1. siehe FLüssigkeitsbild
2. aus dem Flüssigkeitsbild folgt [math]U=\frac{C_1U_{10}+C_2U_{20}}{C_1+C_2}[/math] = 4 V
3. Energieumfsatz gleich Menge mal mittlere Fallhöhe [math]W_{diss}=\Delta QU_{mittel}[/math] = 2.88 mC * 30 V = 86.4 mJ
4. siehe Flowchart

Aufgabe 4

1. Die Summe der Spannungen über den Widerständen 3 und 4 muss gleich 12 V sein. Also ist die Spannung über Widerstand 3 gleich 3 V. Diese Spannung treibt einen Strom der Stärke [math]I_{34}=\frac{U_3}{R_3}[/math] = 0.015 A.
2. Weil 15 mA durch die Widerstände 3 und 4 fliessen, ist die Stromstärke durch die Widerstände 1 und 2 gleich 75 mA. Damit ist der Gesamtwiderstand dieses Zweiges gleich [math]R_{12}=\frac{U_0}{I_{12}}=\frac{12V}{0.075A}[/math] = 160 Ohm.
3. Der Widerstand 1 ergibt sich aus Leistung und Stromstärke [math]R_1=\frac{P}{I_{12}^2}[/math] = 88.9 Ohm. Der zweite Widerstand ist dann die Ergänzung zu 160 Ohm, also gleich 71.1 Ohm.
4. Die Spannung über Widerstand 1 ist gleich [math]U_1=R_1I_{12}[/math] = 6.67 V. Folglich ist die Spannung von A nach B [math]U_{AB}=U_3-U_1[/math] = -3.67 V.

Aufgabenstellung