Aviatik 2013/1: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 20: | Zeile 20: | ||
#Wie gross ist die Ladung des Kondensators nach längerer Zeit? |
#Wie gross ist die Ladung des Kondensators nach längerer Zeit? |
||
#Wie gross ist die Kapazität des Kondensators? |
#Wie gross ist die Kapazität des Kondensators? |
||
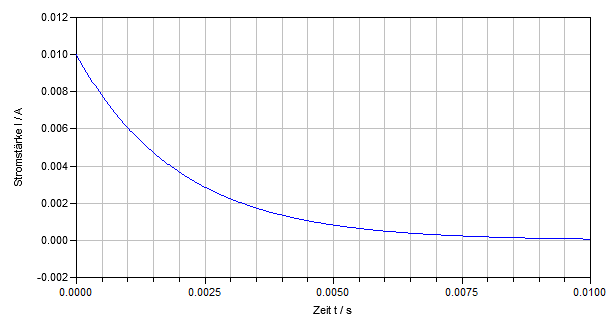
:[[Datei:Aviatik 13_1_2.png|Stromstärke-Zeit-Diagramm]] |
|||
==Aufgabe 3== |
==Aufgabe 3== |
||
Version vom 24. Januar 2014, 13:56 Uhr
Studiengang Aviatik der ZHAW
Erlaubte Hilfsmittel: Taschenrechner, selbst verfasste Formel- und Beispielsammlung ohne Übungsaufgaben, Wörterbuch für fremdsprachige Studierende. Zusätzlich dürfen Sie maximal sechs Seiten (A4) mit Beispielen aus dem Praktikum (ein Modell pro Seite mitnehmen. Diese dürfen die physikalische Analyse mit Variablen und Gesetzen, sowie das Flowchart inkl. Formeln enthalten.
Daten:
- Gravitationsfeldstärke = 9.81 N/kg
- Dichte von Wasser = 1000 kg/m3
Aufgabe 1
Aus einem zylindrischen Gefäss (Querschnitt 0.3 m2 fliesst Wasser durch ein horizontal ausgerichtetes Rohr in ein zweites (Querschnitt 0.7 m2) über. Die Strömung ist turbulent. Anfänglich ist das erste Gefäss zwei Meter hoch gefüllt und das zweite leer. Die Böden der beiden Gefässe liegen auf gleicher Höhe. Die Volumenstromstärke nimmt linear mit der Zeit ab. Nach 600 s sind die beiden Gefässe gleich hoch gefüllt.
- Wie viel Wasser fliesst insgesamt durch das Rohr? Wie stark ist der Volumenstrom zu Beginn des Vorgangs?
- Wie hoch ist das erste Gefäss nach 200 s noch gefüllt?
- Wie viel Energie wird insgesamt dissipiert?
- Wie lange würde es dauern, bis die Niveaus ausgeglichen sind, wenn man den Durchmesser im Rohr verdoppeln würde? Begründen sie Ihre Antwort (mit Formeln, Skizzen oder Argumenten).
Hinweis: Für den turbulenten Strömungswiderstand gilt: [math]k_V=\lambda\frac{8\varrho L}{\pi^2 d^5}[/math]
Aufgabe 2
Zwei gleich grosse Widerstände (je 2 kΩ) bilden einen Spannungsteiler. Parallel zum zweiten Widerstand wird zuerst ein dritter Widerstand (3 kΩ, Teilaufgaben a) und b) ) und danach ein Kondensator (Teilaufgaben c) und d) ) angeschlossen. Alle drei Systeme werden über einen Schalter mit einer Gleichspannungsquelle (20 V) verbunden. Das Diagramm unten zeigt die Stärke des elektrischen Stromes durch den Kondensator in Funktion der Zeit.
- Wie gross ist die Spannung beim grössten Widerstand (R3) in der ersten Anordnung (Skizze).
- Welche Leistung wird dann im ersten Widerstand (R1) dissipiert?
- Wie gross ist die Ladung des Kondensators nach längerer Zeit?
- Wie gross ist die Kapazität des Kondensators?
Aufgabe 3
Der Wagen (totale Masse 400 kg) einer Achterbahn fährt mit 30 m/s in den untersten Punkt eines Vertikalloopings ein (kein Kreis). Jegliche Reibung soll vernachlässigt werden.
- Wie gross muss der Radius an diesem Punkt gewählt werden, damit die Beschleunigung dort 25 m/s2 beträgt?
- Wie gross ist dann die Normalkraft auf den Wagen? Überlegen Sie sich, welche Kräfte auf den Wagen einwirken.
- Der höchste Punkt des Loopings liegt 25 m höher. Wie schnell bewegt sich der Wagen dort?
- Wie gross muss an diesem Punkt der Radius gewählt werden, damit man sich halb so schwer fühlt wie im Ruhezustand auf der Erde?
Aufgabe 4
Ein Güterwagen (Masse 60 t) fährt ungebremst gegen einen zweiten (Masse 30 t), der gebremst ist und anfänglich still steht. Das Diagramm zeigt den Geschwindigkeits-Zeit-Verlauf der beiden Wagen. Die Pufferkraft folgt dem Verlauf einer idealen Feder (linear, keine Reibung).
- Wie gross ist die Reibkraft (Haftreibungs- oder Bremskraft), die auf den zweiten Wagen einwirkt?
- Wie weit bewegt sich der zweite Wagen in der Zeitspanne 0 bis 4 s?
- Wie schnell würde sich der zweite Wagen nach dem Stoss bewegen, wenn er nicht gebremst wäre?
- Wie stark würden die Puffer (hier als Feder mit einer Federkonstanten von 500 kN/m modelliert) im ungebremsten Fall total zusammen gedrückt?
Hinweis: Rechnen Sie mit Hilfe der Energie.
Aufgabe 5
Die Graphik in der 4. Aufgabe ist mit Berkeley-Madonna gerechnet worden. Das zugehörige Modell soll nachfolgend skizziert werden.
- Skizzieren Sie das Systemdiagramm (Flowchart) für diesen Auflaufstoss, so dass die Geschwindigkeiten und die Verschiebung der beiden Wagen berechnet werden können.
- Geben Sie die Gleichungen für die Berechnung der Geschwindigkeiten, der Pufferkraft und der Reibungskraft an, so wie sie für dieses Modell benutzt worden sind. Die Parameter (Masse, Federkonstante, usw.) können Sie mit einem geeigneten Buchstaben angeben.
- Ergänzen Sie das Flowchart um die Energieebene, so dass die kinetische Energie, die Pufferenergie und dissipierte Energie berechnet werden
- Geben Sie alle Gleichungen an, die zur Modellierung der Energiebene benötigt werden (inkl. Anfangswerte für die Energie).