Kraftfluss

Begriff

Unter dem Kraftfluss versteht man den Weg einer Kraft und/oder eines Moments in einem Bauteil vom Angriffspunkt (Stelle der Einleitung!) bis zur Stelle, an der diese durch eine Reaktionskraft und/oder ein Reaktionsmoment aufgenommen werden (Quelle: Vorlesungsunterlagen 2002, Prof. Dr.-Ing. Dr. h. c. mult. Uwe Heisel, Institut für Werkzeugmaschinen, Uni Stuttgart)

Bei der Erarbeitung massstäblicher Entwürfe stellt sich dem Konstrukteur vielfach die Aufgabe, für eine optimale Leitung von Kräften, Drehmomenten und/oder Biegemomenten durch die vorgesehenen Funktionsträger sorgen zu müssen. Zur Veranschaulichung der Funktion "Leiten von Kräften und Momenten" wird gern der Begriff "Kraftfluss" verwendet. (Quelle: Hintzen H., Laufenberg H.:Konstruieren und Berechnen, Vieweg)

Kraftfluss, Kraftleitung: äussere Lasten bewirken Schnittgrössen, die Beanspruchungen (Kräfte, Momente) hervorrufen, welche eleastische oder plastische Verformung hervorrufen. (Quelle: Vorlesungsunterlagen SS 2004 Prof. Dr. Ing. Lucienne Biessing)

Theoretische Grundlagen

In der Punktmechanik kennt man nur Körper und Kräfte, welche zwischen den Körpern wechselwirken. Der Begriff der Kraftleitung ist erst in der technischen Mechanik aufgetaucht, als man mit Hilfe des Schnittprinzips die Konzepte der Newtonschen Punktmechanik und der Eulerschen Starrkörpermechanik auf ausgedehnte Systeme mit einer inneren Struktur übertragen hat.

Zur Beschreibung der Mechanik benötigt man neben der Energie sechs mengenartige oder bilanzierfähige Grössen, die drei Komponenten des Impulses und des Drehimpulses (Nöthersches Theorem). Treten diese sechs Grössen über die materielle Oberfläche eines Körpers, nennt man die zugehörigen Stromstärken Kraft oder Drehmoment. Die drei Kraftkomponenten transformieren sich wie ein Vektor, die drei Komponenten des Drehmomentes wie die drei unabhängigen Komponenten eines schiefsymmetrischen Tensors. Solange man nur eigentliche Transformationen untersucht, verhält sich auch das Drehmoment wie ein Vektor.

Die Stromdichte einer vektorwertige Grösse ist ein Tensor zweiter Stufe; die Stromdichte eines Tensors zweiter Stufe muss mit einem Tensor dritter Stufe beschrieben werden. Nun ist die Stromdichte des Impulses bis auf das Vorzeichen und eine wirkungslose Transposition gleich dem Spannungstensor. Die Stromdichte des Drehimpulsstromes müsste ein spezieller Tensor dritter Stufe sein. Weil in der klassischen Mechanik nur der Impuls lokalisierbar ist, kann für den Drehimpuls aber keine Stromdichte angegeben werden.

Alle in der Literatur gegebenen Definitionen zum Kraftluss sind inkonsistent, weil sie davon ausgehen, dass die vektorwertigen Schnittgrössen Kraft und Drehmoment quasi wie ein Fluss durch die statische Struktur transportiert werden. Nun kann aber nur der Transport einer skalaren Grösse wie Volumen, Masse oder Ladung durch ein einziges Flussbild dargestellt werden.

Impulsstrom

induzierte Wirbelströme

Impuls wird konvektiv und leitungsartig durch den Raum transportiert. Der konvektive Transport, der nur bei Flüssigkeiten und Gasen auftritt, soll hier nicht weiter thematisiert werden. Zur Darstellung des leitungsartigen Impulsstromes nimmt man die Spalten des Spannungstensors, multipliziert diese mit minus eins und zeichnet sie als je einen Pfeil in drei verschiedene Bilder ein. Impulsstrombilder lassen sich problemlos mit Femlab erzeugen. Zu beachten ist, dass die konkrete Gestalt der drei Strombilder von der Wahl des Koordinatensystems abhängt.

x- und y-Impulsstrom in einem Stück Blech

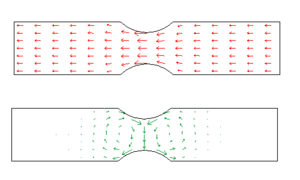
Das erste Bild zeigt den Impulsstrom durch einen beidseits eingekerbten Blechstreifen. Im Bereich der Kerben wird der primäre Impulsstrom gegen die Mitte hin abgelenkt. Dabei entstehen Wirbelströme der zweiten Impulskomponente. Schuld an dieser Wirbelbildung ist das Prinzip der zugeordneten Schubspannung (Symmetrie des Spannungstensors). In der Sprache der Impulsströme besagt dieses Prinzip, dass ein y-Impulsstrom in x-Richtung fließen muss, sobald der x-Impulsstrom in die y-Richtung ausweicht. Allgemein formuliert muss die j-Komponente der i-Impulsstromdichte an jedem Ort gleich der i-Komponente der j-Impulsstromdichte sein (i und j stehen für x, y und z).

Prinzip der direkten Kraftleitung

Das Prinzip der direkten Kraftleitung besagt, dass die Kraft in ihre eigene Wirkrichtung „abgeleitet“ werden soll. Übersetzt man diese Aussage ins Impulsstrombild, bedeutet dies, dass jede Impulskomponente möglichst in ihre eigene Richtung strömen soll. Andernfalls werden Wirbelströme induziert. Diese Übersetzung vom Kraft- ins Impulsstrombild trifft jedoch nur zu, wenn eine Achse des globalen Koordinatensystems mit der Kraftrichtung zusammenfällt. Nur dann fließt bei reiner Zug- oder Druckbelastung eine einzige Impulskomponente in ihre eigene Bezugsrichtung. Bei allgemeiner Ausrichtung fließen zwei oder sogar drei Impulskomponenten gleichzeitig durch das unter Zug- oder Druck stehende Bauteil. Das Dilemma zwischen nur global gültigem Strombild und lokaler Analyse bezüglich der Hauptspannungsrichtung lässt sich durch Einführung von bauteilspezifischen Koordinatensystemen lösen. Im einfachsten Fall der Zug- und Druckstäbe reduziert sich das lokale Koordinatensystem auf einen Bezugspfeil. Wie man damit umgeht, kann anhand einfacher Fachwerk gezeigt werden.

Prinzip der kurzen Kraftleitung

Der Kraftfluss soll direkt und kurz geführt sein. Direkt und kurz geführte Kraftflüsse verursachen keine unnötigen Wirbel. Muss der in einem Zugstab in seine eigene Bezugsrichtung fließende Impulsstrom aus konstruktiven Gründen umgeleitet werden, induziert er gemäß dem Prinzip der zugeordneten Schubspannung einen zusätzlichen Strom. Im Kopplungsgebiet fließen Primär- und Sekundärstrom mit der gleichen Stromdichte in die Richtung der jeweils andern Komponenten. Weil der Sekundärstrom nicht durch die Oberfläche des Bauteils treten kann, schließt er sich im Innern des Bauteils zu einem Kreis.

Datei:Kraftfluss Bügel x.gif

x-Impulsstrom in einem offenen Bügel

Datei:Kraftfluss Bügel y.gif

y-Impulsstrom in einem offenen Bügel

Die Wirbelbildung soll nun anhand eines einfachen Beispiels diskutiert werden. Ersetzt man einen Teil eines Zugstabes durch einen offenen Bügel, muss der primäre Impulsstrom in den Armen des Bügels seitwärts zu seiner Bezugsrichtung fließen. Dabei induziert er gemäß dem Gesetz der zugeordneten Schubspannungen zwei Sekundärströme, die sich über den beiden Armen des Bügels zu je einem Wirbel schließen. In beiden Ecken des Bügels fließen die Sekundärströme seitwärts und induzieren dabei einen Tertiärstrom, der sich über den mittleren Teil des Bügels zu einem Wirbel schließt. Primär- und Tertiärstrom transportieren die gleiche Impulskomponente und bilden zusammen einen Gesamtstrom (oberes Bild). Im unteren Bild kann man die zwei Wirbelströme der Sekundärkomponente deutlich erkennen.