Zwei Petflaschen: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) (→Modell) |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
==System== |
==System== |
||
[[Bild: ZweiFlaschen.jpg|thumb|Druckausgleich in Petflaschen]] |
[[Bild: ZweiFlaschen.jpg|thumb|Druckausgleich in Petflaschen]] |
||
Zwei Petflaschen (Fassungsvermögen je 1.5 Liter) werden über |
Zwei Petflaschen (Fassungsvermögen je 1.5 Liter) werden über einen Polyamidschlauch (Länge 1.5 m, Innendurchmesser 2 mm) miteinander verbunden. Die eine Flasche ist bei einem Absolutdruck von 5 bar mit 1.2 Liter Wasser gefüllt, die andere enthält nur Luft bei Umgebungsdruck. Nach dem Öffnen des Hahns findet ein Druckausgleich statt. |
||
==Modell== |
==Modell== |
||
| ⚫ | |||
Ausgehend von der Volumenbilanz wird der Druck in beiden Flaschen berechnet. Die Flaschen werden als Blasenspeicher modelliert. Die Druckdifferenz treibt dann den Volumenstrom, der bei grosser Stromstärke durch einen turbulenten und bei langsamer Strömung durch einen laminaren Widerstand begrenzt wird. Turbulenter und laminarer Widerstand sind gemäss den Formeln der [[Hydrodynamik]] berechnet worden. Mit der Bedingung |
Ausgehend von der Volumenbilanz wird der Druck in beiden Flaschen berechnet. Die Flaschen werden als Blasenspeicher modelliert. Die Druckdifferenz treibt dann den Volumenstrom, der bei grosser Stromstärke durch einen turbulenten und bei langsamer Strömung durch einen laminaren Widerstand begrenzt wird. Turbulenter und laminarer Widerstand sind gemäss den Formeln der [[Hydrodynamik]] berechnet worden. Mit der Bedingung |
||
IV = IF delta_p<delta_pkrit THEN delta_p/RV ELSE SQRT(delta_p/k) |
IV = IF delta_p<delta_pkrit THEN delta_p/RV ELSE SQRT(delta_p/k) |
||
wird sicher gestellt, dass |
wird sicher gestellt, dass sich die Volumenstromstärke im unterkritischen Bereich proportional zur Druckdifferenz ändert, darüber aber nur noch mit der Wurzel aus derselben zunimmt. |
||
| ⚫ | |||
Auf einer zweiten Ebene wird die Energiebetrachtung modelliert. Die zugeordneten Energieströme werden zur Änderung der Speicherenergie und die Prozessleistung zur total dissipierten Energie aufintegriert. |
Auf einer zweiten Ebene wird die Energiebetrachtung modelliert. Die zugeordneten Energieströme werden zur Änderung der Speicherenergie und die Prozessleistung zur total dissipierten Energie aufintegriert. |
||
| ⚫ | |||
| ⚫ | |||
==Simulation== |
==Simulation== |
||
Im Volumenstromstärke-Zeit-Diagramm ist der Punkt, an dem die Strömung von turbulent auf laminar umschaltet, deutlich erkennbar. Ein erster Vergleich mit der Messung hat gezeigt, dass die Widerstände grösser als die in der Simulation angenommenen sein müssen. |
|||
<gallery caption="Ergebnisse"> |
|||
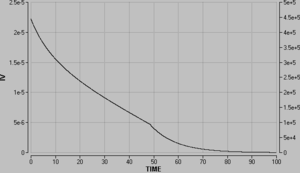
[[Bild: Petflaschen_IV.png|thumb|left|Volumenstromstärke-Zeit-Diagramm]] |
|||
Bild:Rotkehlchen_gr.jpg|Rotkehlchen |
|||
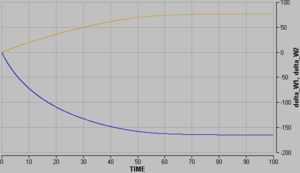
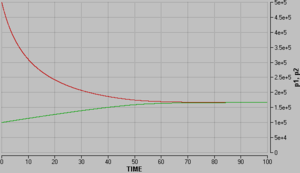
[[Bild: Petflaschen_p.png|thumb|center|Druck-Zeit-Diagramme]] |
|||
Bild:Gaense2004.jpg|Gänse |
|||
Bild:Waran.jpg|Komodowaran |
|||
Bild:Cat outside.jpg|Hauskatze |
|||
</gallery> |
|||
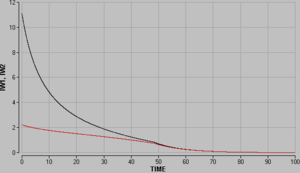
Aus den zugeordneten Energieströmen kann nur die Änderung der Speicherenergie direkt berechnet werden. Die absolute Skalierung der hydraulisch gespeicherten Energie müsste über den Anfangswert vorgenommen werden. Um Vorzeichenprobleme zu vermeiden, sollte die Orientierung der Energieströme mit denen der Volumenströme übereinstimmen. |
|||
[[Bild: Petflaschen_IW.png|thumb|left|Energiestromstärke-Zeit-Diagramme]] |
|||
[[Bild: Petflaschen_W.png|thumb|center|Energieänderung-Zeit-Diagramme]] |
|||
Version vom 9. Oktober 2006, 20:05 Uhr
System
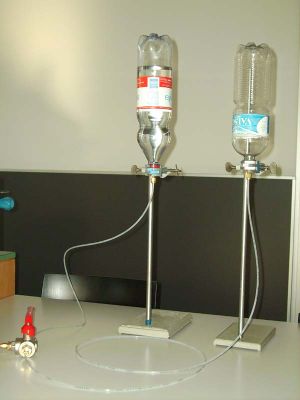
Zwei Petflaschen (Fassungsvermögen je 1.5 Liter) werden über einen Polyamidschlauch (Länge 1.5 m, Innendurchmesser 2 mm) miteinander verbunden. Die eine Flasche ist bei einem Absolutdruck von 5 bar mit 1.2 Liter Wasser gefüllt, die andere enthält nur Luft bei Umgebungsdruck. Nach dem Öffnen des Hahns findet ein Druckausgleich statt.
Modell
Ausgehend von der Volumenbilanz wird der Druck in beiden Flaschen berechnet. Die Flaschen werden als Blasenspeicher modelliert. Die Druckdifferenz treibt dann den Volumenstrom, der bei grosser Stromstärke durch einen turbulenten und bei langsamer Strömung durch einen laminaren Widerstand begrenzt wird. Turbulenter und laminarer Widerstand sind gemäss den Formeln der Hydrodynamik berechnet worden. Mit der Bedingung
IV = IF delta_p<delta_pkrit THEN delta_p/RV ELSE SQRT(delta_p/k)
wird sicher gestellt, dass sich die Volumenstromstärke im unterkritischen Bereich proportional zur Druckdifferenz ändert, darüber aber nur noch mit der Wurzel aus derselben zunimmt.
Auf einer zweiten Ebene wird die Energiebetrachtung modelliert. Die zugeordneten Energieströme werden zur Änderung der Speicherenergie und die Prozessleistung zur total dissipierten Energie aufintegriert.


Simulation
Im Volumenstromstärke-Zeit-Diagramm ist der Punkt, an dem die Strömung von turbulent auf laminar umschaltet, deutlich erkennbar. Ein erster Vergleich mit der Messung hat gezeigt, dass die Widerstände grösser als die in der Simulation angenommenen sein müssen.
Aus den zugeordneten Energieströmen kann nur die Änderung der Speicherenergie direkt berechnet werden. Die absolute Skalierung der hydraulisch gespeicherten Energie müsste über den Anfangswert vorgenommen werden. Um Vorzeichenprobleme zu vermeiden, sollte die Orientierung der Energieströme mit denen der Volumenströme übereinstimmen.