Plattenkondensator: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 8: | Zeile 8: | ||
==Kapazität== |
==Kapazität== |
||
Ist die Plattendiagonale viel grösser als der Plattenabstand, darf das elektrische Feld als homogen betrachtet werden. Im homogenen Feld ist die Spannung gleich |
Ist die Plattendiagonale viel grösser als der Plattenabstand, darf das elektrische Feld als homogen betrachtet werden. Im homogenen Feld ist die Spannung gleich Feldstärke mal Distanz in Feldrichtung |
||
<math>U = Ed</math> |
<math>U = Ed</math> |
||
Die Ladungen auf den Platten bilden |
Die Ladungen auf den Platten bilden Quellen bzw. Senken des elektrischen Feldes. Die Feldstärke ist proportional zur Flächenladungsdichte ''σ'' |
||
<math>E = \frac {\sigma}{\epsilon_0}</math> |
<math>E = \frac {\sigma}{\epsilon_0}</math> |
||
| Zeile 21: | Zeile 21: | ||
<math>C = \frac {Q}{U} = \frac {A \sigma}{\frac {\sigma}{\epsilon_0}d} = \epsilon_0 \frac {A}{d}</math> |
<math>C = \frac {Q}{U} = \frac {A \sigma}{\frac {\sigma}{\epsilon_0}d} = \epsilon_0 \frac {A}{d}</math> |
||
==Energiedichte== |
|||
Die Energie des [[Kondensator|Kondensators]] wächst quadratisch mit der Ladung |
|||
<math>W = \frac {1}{2} Q U = \frac {Q^2}{2C}</math> |
|||
Diese Energie ist im elektrischen Feld des Kondensators gespeichert. Nimmt man nun an, dass das elektrische Feld des Kondensators homogen ist und sich nur auf den Raum zwischen den Platten erstreckt, kann die Energiedichte des elektrischen Feldes berechnet werden. Rein formal schreibt sich die Energie des homogenen Feldes als Energiedichte mal Volumen |
|||
<math>W = \rho_W V = \rho_W A d</math> |
|||
Ersetzt man nun in der Berechnungsformel für die Energie des Kondensators die Ladung durch Oberlächenladungsdichte (''σ'') mal Oberfläche der einen Platte (''A'') und schreibt für die Spannung Feldstärke mal Distanz, erhält man die Energie des Plattenkondensators in Funktion der Feldstärke |
|||
<math>W = \frac {1}{2} Q U = \frac {1}{2}A \sigma E d = \frac {1}{2} \epsilon_0 E^2 A d</math> |
|||
Durch Vergleich der beiden Formeln für die Energie erhält man die Energiedichte im homogenen Feld des Plattenkondensators |
|||
<math>\rho_W = \frac {1}{2} \epsilon_0 E^2</math> |
|||
Weil sowohl Energiedichte als auch Feldstärke lokale Grössen sind, gilt diese Beziehung an jedem Ort eines beliebigen elektrischen Feldes. |
|||
==Dielektrikum== |
|||
[[Kategorie: Elektro]] |
[[Kategorie: Elektro]] |
||
Version vom 1. Dezember 2006, 05:56 Uhr
Bauform
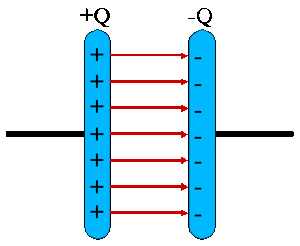
Der einfach Plattenkondensator besteht aus zwei metallischen Platten, die sich in möglichst geringem Abstand gegenüber stehen. Bringt man nun elektrische Ladung auf die eine Platte und erdet die andere, wird auf der zweiten Platte infolge Influenz die gleiche Ladungsmenge verdrängt wie auf die erste aufgebracht worden ist.
Füllt man den Raum zwischen den Platten mit einem Isolator (Dielektrikum) auf, kann der Plattenabstand sehr klein gemacht werden. Dies erhöht die Kapazität des Kondensators. Weil das Isoliermaterial polarisierbar ist, bilden sich an der Oberfläche des Dielektrikums Oberflächenladungen, die das von den Platten erzeugte elektrische Feld abschwächen. Dieser Effekt vergrössert die Kapazität des Kondensators zusätzlich.
Plattenkondensatoren erlauben in modifizierter Ausführung sehr hohe Kapazitäten pro Volumen. Indem man die jeweils mit einem Potential verbundenen Elektroden abwechselnd aufeinander stapelt, werden sie doppelt wirksam. Sind die Platten als Metallfolie oder -film ausgeführt, können sie bei einem geeigneten Isolator aufgewickelt werden. Aufgrund seiner kompakten Bauform ist dies der gebräuchlichste Kondensator.
Kapazität
Ist die Plattendiagonale viel grösser als der Plattenabstand, darf das elektrische Feld als homogen betrachtet werden. Im homogenen Feld ist die Spannung gleich Feldstärke mal Distanz in Feldrichtung
[math]U = Ed[/math]
Die Ladungen auf den Platten bilden Quellen bzw. Senken des elektrischen Feldes. Die Feldstärke ist proportional zur Flächenladungsdichte σ
[math]E = \frac {\sigma}{\epsilon_0}[/math]
wobei ε0 für die elektrische Feldkonstante steht.
Setzt man diese Beziehunen in die Definitionsgleichung der Kapazität ein, erhält man die Berechnungsformel für einen Plattenkondensator
[math]C = \frac {Q}{U} = \frac {A \sigma}{\frac {\sigma}{\epsilon_0}d} = \epsilon_0 \frac {A}{d}[/math]
Energiedichte
Die Energie des Kondensators wächst quadratisch mit der Ladung
[math]W = \frac {1}{2} Q U = \frac {Q^2}{2C}[/math]
Diese Energie ist im elektrischen Feld des Kondensators gespeichert. Nimmt man nun an, dass das elektrische Feld des Kondensators homogen ist und sich nur auf den Raum zwischen den Platten erstreckt, kann die Energiedichte des elektrischen Feldes berechnet werden. Rein formal schreibt sich die Energie des homogenen Feldes als Energiedichte mal Volumen
[math]W = \rho_W V = \rho_W A d[/math]
Ersetzt man nun in der Berechnungsformel für die Energie des Kondensators die Ladung durch Oberlächenladungsdichte (σ) mal Oberfläche der einen Platte (A) und schreibt für die Spannung Feldstärke mal Distanz, erhält man die Energie des Plattenkondensators in Funktion der Feldstärke
[math]W = \frac {1}{2} Q U = \frac {1}{2}A \sigma E d = \frac {1}{2} \epsilon_0 E^2 A d[/math]
Durch Vergleich der beiden Formeln für die Energie erhält man die Energiedichte im homogenen Feld des Plattenkondensators
[math]\rho_W = \frac {1}{2} \epsilon_0 E^2[/math]
Weil sowohl Energiedichte als auch Feldstärke lokale Grössen sind, gilt diese Beziehung an jedem Ort eines beliebigen elektrischen Feldes.