Feuerwehrspritze

Vor hundert Jahren besass praktisch jede Feuerwehr eine Handdruckspritze. Eine Feuerspritze oder Handdruckspritze ist eine mit Muskelkraft betriebene Feuerlöschpumpe, welche zur Brandbekämpfung verwendet wird.

Die erste Feuerspritze wurde von Ktesibios im 3. Jahrhundert v. Chr. konstruiert. Im antiken Rom gab es schon eine organisierte Feuerwehr, zu deren Ausrüstung neben Eimern, Äxten und anderem auch eine Feuerspritze gehörte, die nach dem Prinzip der Druckpumpe funktionierte. Wie viele Erfindungen der Antike musste auch die Feuerspritze neu erfunden werden. Dies gelang 1655 einem Nürnberger Zirkelschmied, bei dessen Konstruktion etwa 16-20 Mann mit einer Hebelstange das Wasser durch ein langes Holzrohr pumpten.

schematische Darstellung einer Handdruckspritze

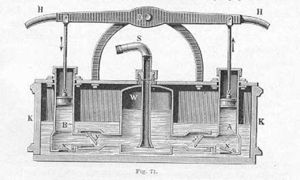
Feuerspritzen gehörten im 19. Jahrhundert häufig zur Ausstattung der Feuerwehren. Die Norm sah zu dieser Zeit 1888 folgende Eigenschaften vor:

• 100 Millimeter weite Zylinder
• eine Förderung von 170 bis 190 Liter Wasser bei 30 bis 35 Doppelhüben in der Minute
• 8 Meter Saughöhe
• 28 bis 29 Meter Strahlweite
• 23 Meter Strahlhöhe
• Verschraubung der Druckschläuche mit Normalgewinde
• das Spritzwerk muss einem Wasserdruck von 12 kg auf den Quadratzentimeter drei Minuten widerstehen.

Mit der technischen Weiterentwicklung der Feuerlöschgeräte verloren die Feuerspritzen zunehmend ihre Aufgabe in der aktiven Brandbekämpfung. Heute sind jedoch noch viele Exemplare in Museen zu finden. Auch einige Feuerwehren pflegen noch ihre teils funktionstüchtigen Geräte.

Theorie

Am schweizerischen Handdruckspritz-Wettbewerg in Rohrbach (15. Mai 1999) hat die Mannschaft alte Spritze Niederglatt den 23. Rang erreicht. Folgende Daten sind verfügbar: Zylinderzahl 2, Bohrung 140 mm, Hub 270 mm, Wassermenge in 4 Minuten 1359 Liter, Wurfweite 25 m.

Modelliert man den Wurf ideal symmetrisch, kann die Ausströmgeschwindigkeit aus dem Strahlrohr und daraus der Überdruck im Kessel einfach abgeschätzt werden

Wurfparabel: [math]y(x) = \tan(\alpha) - \frac{g}{2 v_0^2 \cos^2(\alpha)} x^2[/math]

für y = 0 und α = 45°: [math]x = frac {v_0^2}{g}[/math] oder [math]v_0 = \sqrt(xg)[/math] = 15.7 m/s

Überdruck: [math]p_e = \frac {\rho}{2} v_0^2 = \frac {xg}{2}[/math] = 1.23 bar

Aus der mittleren Volumenstromstärke (5.66 l/s) und der Ausströmgeschwindigkeit (15.7 m/s) kann der Durchmesser des Wasserstrahles (21 mm) abgeschätzt werden. Bei voller Hubausschöpfung wird mit jedem Doppelhub eine Wassermenge von 8.31 Litern in den Windkessel gedrückt. Somit sind 163 Hübe notwendig, um die Wassermenge von 1359 Liter zu pumpen. Dies ergibt eine Frequenz von 0.68 Hz.

Simulationsmodell

Systemdiagramm der Handdruckspritze

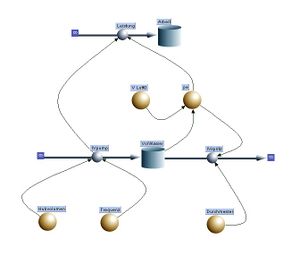
Der zufliessende Volumenstrom ist als Betrag einer Sinusfunktion (Amplitude gleich pi mal einfaches Hubvolumen mal Frequenz) modelliert worden. Der einzige frei Parameter, das Volumen des Windkessels, ist auf 20 Liter gesetzt worden.

Simulationsergebnisse

Volumenstromstärken vor und nach dem Windkessel

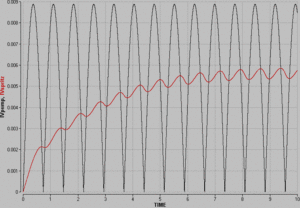
Der Vergleich zwischen zu- und abfliessender Volumenstromstärke zeigt die glättende Wirkung des Windkessels (hydraulische Kapazität).

Leistung bezüglich des Wasserstromes

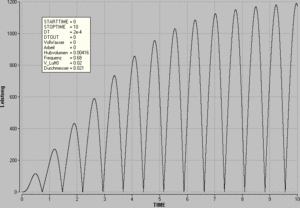
Die Leistung erreicht maximal 1.2 kW.