Lösung zu Vollelastischer Stoss: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:VollelastischerStoss.png|thumb|Flüssigkeitsbild]] |
[[Bild:VollelastischerStoss.png|thumb|Flüssigkeitsbild]] |
||
#Beim total inelastischen Stoss gleicht sich die "Füllhöhe" aus <math>v_{in} = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} = \frac{1.5 kg * 2.4 m/s + 6 kg * 0.8 m/s}{7.5 kg} = 1.12 m/s</math> |
#Beim total inelastischen Stoss gleicht sich die "Füllhöhe" aus <math>v_{in} = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} = \frac{1.5 kg * 2.4 m/s + 6 kg * 0.8 m/s}{7.5 kg} = 1.12 m/s</math> |
||
#Beim vollständig elastischen Stoss wird zusätzlich nochmals so viel Impuls hinaufgepumpt, wie vorher hinunter geflossen ist. Im ersten Fahrzeug nimmt die Geschwindigkeit um 1.28 m/s ab, bis beide Fahrzeuge gleich schnell sind. Folglich nimmt die Geschwindigkeit im elastischen Fall nochmals um soviel auf -0. |
#Beim vollständig elastischen Stoss wird zusätzlich nochmals so viel Impuls hinaufgepumpt, wie vorher hinunter geflossen ist. Im ersten Fahrzeug nimmt die Geschwindigkeit um 1.28 m/s ab, bis beide Fahrzeuge gleich schnell sind. Folglich nimmt die Geschwindigkeit im elastischen Fall nochmals um soviel auf -0.16 m/s ab, bis die Fahrzeuge auseinander fahren. Die Geschwindigkeit nimmt im zweiten Fahrzeug analog daz von 0.8 m/s auf 1.12 m/s und dann nochmals um 0.32 m/s auf 1.44 m/s zu. |
||
'''[[Vollelastischer Stoss|Aufgabe]]''' |
'''[[Vollelastischer Stoss|Aufgabe]]''' |
||
Version vom 9. Januar 2007, 07:58 Uhr
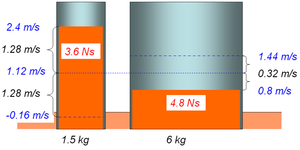
- Beim total inelastischen Stoss gleicht sich die "Füllhöhe" aus [math]v_{in} = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} = \frac{1.5 kg * 2.4 m/s + 6 kg * 0.8 m/s}{7.5 kg} = 1.12 m/s[/math]
- Beim vollständig elastischen Stoss wird zusätzlich nochmals so viel Impuls hinaufgepumpt, wie vorher hinunter geflossen ist. Im ersten Fahrzeug nimmt die Geschwindigkeit um 1.28 m/s ab, bis beide Fahrzeuge gleich schnell sind. Folglich nimmt die Geschwindigkeit im elastischen Fall nochmals um soviel auf -0.16 m/s ab, bis die Fahrzeuge auseinander fahren. Die Geschwindigkeit nimmt im zweiten Fahrzeug analog daz von 0.8 m/s auf 1.12 m/s und dann nochmals um 0.32 m/s auf 1.44 m/s zu.