Biegung: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
==Drehimpulstransport== |
==Drehimpulstransport== |
||
[[Bild:DrehimpulsstromBiegung.png|thum|Drehimpulsstrom und Impulsstrom bei Biegung]] |
|||
Der [[Drehimpulsstrom]] kann nicht direkt gemessen werden. In ruhenden Systeme wird der Drehimpulsstrom aber immer durch [[Impulsstrom|Impulsströme]] berandet. Die Stärke dieser Impulsströme kann mit Hilfe der Verformung des durchflossene Material gemessen werden ([[Federwaage]], [[Kraftmessdose]]). Damit ein Drehimpuls seitwärts zu seiner Bezugsrichtung fliessen kann, muss der Transport beidseits durch Impulsströme begrenzt sein. Fliesst zum Beispiel ''y''-Drehimpuls in die positive ''x''-Richtung, fliesst auf der einen Seite ''x''-Impuls in Richtung der''x''-Achse (Druck) und auf der andern Seite gegen die ''x''-Achse (Zug). Das Bild zeigt wie der ''x''-Impuls- (rot) und der ''y''-Drehimpuls (blau) durch den gebogenen Balken fliessen. |
|||
Zwischen der Drehimpulsstromdichte ''j<sub>Lyx</sub>'' und der Impulsstromdichte ''j<sub>pxx</sub>'' besteht eine spezielle Gradientenbeziehung |
|||
<math>j_{Lyx,z} = -j_{pxx}</math> |
<math>j_{Lyx,z} = -j_{pxx}</math> |
||
Version vom 10. Januar 2007, 12:46 Uhr
Biegung tritt auf, wenn ein Körper von seitwärts fliessenden Drehimpuls durchströmt wird. Die Stärke dieses Drehimpulsstromes bezüglich einer ausgewählten Querschnittfläche nennt man Biegemoment. In der Regel untersucht man die Biegung prismatischer Körper (Balken, Vierkantrohr, U-, T- oder H-Balken). Hier wird angenommen, dass die x-Achse in Richtung des Balkens zeigt und dass y-Drehimpuls durch den Balken transportiert wird.
Drehimpulstransport
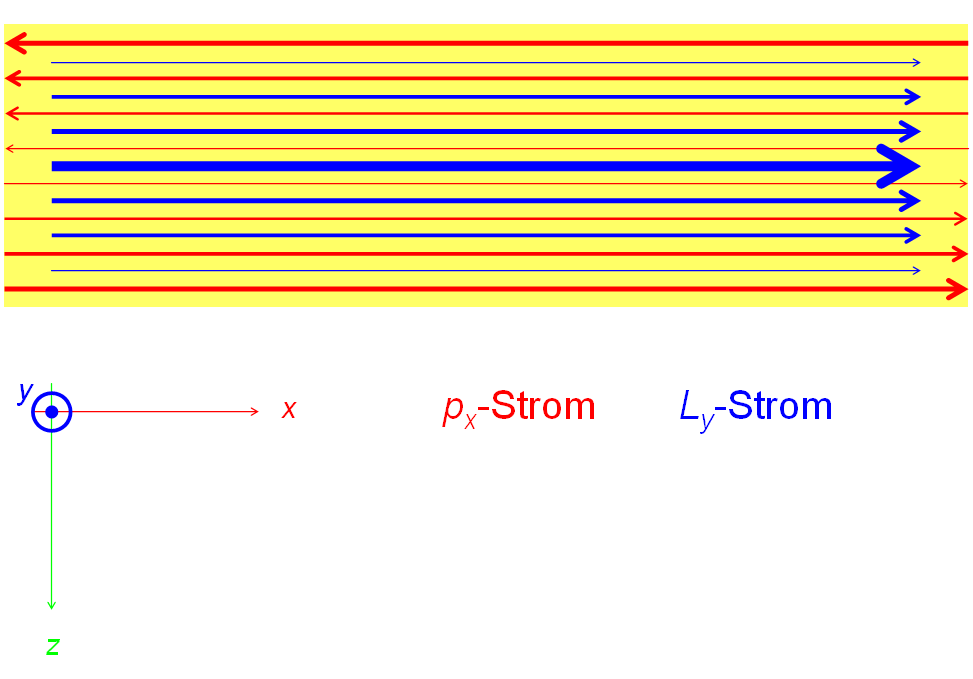Der Drehimpulsstrom kann nicht direkt gemessen werden. In ruhenden Systeme wird der Drehimpulsstrom aber immer durch Impulsströme berandet. Die Stärke dieser Impulsströme kann mit Hilfe der Verformung des durchflossene Material gemessen werden (Federwaage, Kraftmessdose). Damit ein Drehimpuls seitwärts zu seiner Bezugsrichtung fliessen kann, muss der Transport beidseits durch Impulsströme begrenzt sein. Fliesst zum Beispiel y-Drehimpuls in die positive x-Richtung, fliesst auf der einen Seite x-Impuls in Richtung derx-Achse (Druck) und auf der andern Seite gegen die x-Achse (Zug). Das Bild zeigt wie der x-Impuls- (rot) und der y-Drehimpuls (blau) durch den gebogenen Balken fliessen.
Zwischen der Drehimpulsstromdichte jLyx und der Impulsstromdichte jpxx besteht eine spezielle Gradientenbeziehung
[math]j_{Lyx,z} = -j_{pxx}[/math]
Die Symbolik ,z steht für die partielle Ableitung nach der z-Koordinate.