Lösung zu Puffer-Prüfstand: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Version vom 4. Februar 2007, 10:41 Uhr

Der schwerere Wagen stehe links, die positive Richtung zeige nach rechts.

Die Hydraulik fördert zuerst Impuls vom rechten in den linken Wagen. Die Stangen werden auf Zug belastet, weil der Impuls gegen die Bezugsrichtung fliesst. Beim Aufprall strömt der Impuls durch die Puffer vom linken in den rechten Wagen zurück. Sobald die Wagen still stehen, sind die Puffer voll eingefahren. Beim Ausfahren der Puffer wird - vor allem durch die Wirkung der Ringfeder - zusätzlich Impuls vorwärts, also von links nach rechts gepumpt. Deshalb fahren die Wagen zurück. Am Schluss werden die Wagen von der Hydraulik abgebremst. Dabei fliesst nochmals Impuls von rechts nach links durch die Zugstangen der Hydraulik.

Bei der Schwab-Methode bleibt der Massenmittelpunkt des Gesamtsystems immer in Ruhe. Die Hydraulik muss nur soviel Energie aufwenden, wie die Puffer im Idealfall aufnehmen. Lässt man dagegen nur einen Wagen gegen einen ruhenden rollen, ist die kinetische Energie des Hammerwagens anfänglich grösser als die von den Puffern aufzunehmende Energie, wie aus dem Flüssigkeitsbild klar hervorgeht.
Die Stärke des durch die Puffer fliessenden Impulsstromes erreicht eine Stärke von knapp 1000 kN. Folglich sollte die Beschleunigung der Wagen (Impulsänderungsrate geteilt durch die Masse) höchstens 22.2 m/s² und 25m/s² betragen.
Die Puffer haben eine relativ kleine Masse, der Impuls strömt also direkt von einem Wagen in den andern und die "Pufferkraft" ist bei beiden Puffern zu jedem Zeitpunkt gleich gross. Nun geht der Ringfederpuffer schon bei etwa 600 kN auf Block. Die Einfahrgeschwindigkeit dieses Puffers geht dann sehr rasch gegen Null. Folglich ist der Hydraulikpuffer plötzlich mit einer grösseren Geschwindigkeitsdifferenz konfrontiert und reagiert entsprechend steifer.
Die von den Puffern aufgenommene Energie entspricht der Fläche unter der Kurve im Kraft-Hub-Diagramm.
Anfänglich bewegen sich die Wagen im umgekehrten Verhältnis ihrer Massen aufeinander zu, also mit 1.9 m/s und 1.69 m/s. Weil der Massenmittelpunkt in Ruhe bleibt, ist die von den Puffern maximal aufzunehmende Energie gleich der Summe der beiden kinetischen Energien, als gleich 64.3 kJ und 72.2 kJ. Davon übernehmen die Wagen den Teil, der sich bei den Puffern nicht nachweisen lässt:W_Wagen = 64.3 kJ + 72.2 kJ - (63.4 kJ - 33.6 kJ) = 39.5 kJ. Dieser relativ grosse Anteil hängt mit Schlag zusammen, der entsteht, wenn der Ringfederpuffer auf Block geht. Dann rutscht die Ladung (Betonklötze) trotz massiver Befestigung ein wenig.

Aufgabe

@@ Zeile 1: / Zeile 1: @@
 Der schwerere Wagen stehe links, die positive Richtung zeige nach rechts.
-#Die Hydraulik fördert zuerst Impuls vom rechten in den linken Wagen. Die Stangen werden auf Zug belastet, weil der Impuls gegen die Bezugsrichtung fliesst. Beim Aufprall strömt der Impuls durch die Puffer vom linken in den rechten Wagen zurück. Sobald die Wagen still stehen, sind die Puffer voll eingefahren. Beim Ausfahren wird - vor allem durch die Wirkung der Ringfeder - zusätzlich Impuls vorwärts, also von links nach rechts gepumpt. Danach fahren die Wagen zurück. Am Schluss werden die Wagen von der Hydraulik abgebremst. Dabei fliesst nochmals Impuls von rechts nach links durch die Zugstangen der Hydraulik.
+#Die Hydraulik fördert zuerst Impuls vom rechten in den linken Wagen. Die Stangen werden auf Zug belastet, weil der Impuls gegen die Bezugsrichtung fliesst. Beim Aufprall strömt der Impuls durch die Puffer vom linken in den rechten Wagen zurück. Sobald die Wagen still stehen, sind die Puffer voll eingefahren. Beim Ausfahren der Puffer wird - vor allem durch die Wirkung der Ringfeder - zusätzlich Impuls vorwärts, also von links nach rechts gepumpt. Deshalb fahren die Wagen zurück. Am Schluss werden die Wagen von der Hydraulik abgebremst. Dabei fliesst nochmals Impuls von rechts nach links durch die Zugstangen der Hydraulik.
+[[Bild:Puffer_Pruefstand_FB.png|thumb|Flüssigkeitsbild der beiden Methoden]]
-#Bei der Schwab-Methode bleibt der Massenmittelpunkt des Gesamtsystems immer in Ruhe. Die Hydraulik muss nur soviel Energie aufwenden, wie die Puffer im Idealfall aufnehmen. Lässt man einen Wagen gegen einen ruhenden rollen, ist die kinetische Energie des Hammerwagens anfänglich grösser als die von den Puffern aufzumehmende, wie aus dem [[Flüssigkeitsbild]] klar hervorgeht.
+#Bei der Schwab-Methode bleibt der Massenmittelpunkt des Gesamtsystems immer in Ruhe. Die Hydraulik muss nur soviel Energie aufwenden, wie die Puffer im Idealfall aufnehmen. Lässt man dagegen nur einen Wagen gegen einen ruhenden rollen, ist die kinetische Energie des Hammerwagens anfänglich grösser als die von den Puffern aufzunehmende Energie, wie aus dem [[Flüssigkeitsbild]] klar hervorgeht.
 #Die Stärke des durch die Puffer fliessenden Impulsstromes erreicht eine Stärke von knapp 1000 kN. Folglich sollte die Beschleunigung der Wagen (Impulsänderungsrate geteilt durch die Masse) höchstens 22.2 m/s<sup>2</sup> und 25m/s<sup>2</sup> betragen.
-#Die Puffer haben eine relativ kleine Masse. Deshalb fliesst der Impuls direkt von einem Wagen in den andern; die "Pufferkraft" ist bei beiden Puffern zu jedem Zeitpunkt gleich gross. Nun geht der Ringfederpuffer schon bei etwa 600 kN auf Block. Die Einfahrgeschwindigkeit dieses Puffers fällt dann praktisch schlagartig auf Null. Folglich ist der Hydraulikpuffer plötzlich mit einer grösseren Geschwindigkeitsdifferenz konfrontiert und reagiert entsprechend steifer.
+#Die Puffer haben eine relativ kleine Masse, der Impuls strömt also direkt von einem Wagen in den andern und die "Pufferkraft" ist bei beiden Puffern zu jedem Zeitpunkt gleich gross. Nun geht der Ringfederpuffer schon bei etwa 600 kN auf Block. Die Einfahrgeschwindigkeit dieses Puffers geht dann sehr rasch gegen Null. Folglich ist der Hydraulikpuffer plötzlich mit einer grösseren Geschwindigkeitsdifferenz konfrontiert und reagiert entsprechend steifer.
 #Die von den Puffern aufgenommene Energie entspricht der Fläche unter der Kurve im Kraft-Hub-Diagramm.
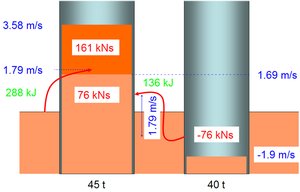
-#Anfänglich bewegen sich die Wagen im umgekehrten Verhältnis ihrer Massen aufeinander zu, also mit 1.9 m/s und 1.69 m/s. Weil der Massenmittelpunkt in Ruhe bleibt, ist die von den Puffern maximal aufzunehmende Energie gleich der Summe der beiden kinetischen Energien, als gleich 64.3 kJ und 72.2 kJ. Davon übernehmen die Wagen den Teil, der sich bei den Puffern nicht nachweisen lässt:''W''<sub>Wagen</sub> = 64.3 kJ + 72.2 kJ - (63.4 kJ - 33.6 kJ) = 39.5 kJ. Dieser relativ grosse Anteil hängt mit Schlag zusammen, der entsteht, wenn der Ringfederpuffer auf Block geht. Dann rutscht auch die Ladung trotz massiver Befestigung ein wenig.
+#Anfänglich bewegen sich die Wagen im umgekehrten Verhältnis ihrer Massen aufeinander zu, also mit 1.9 m/s und 1.69 m/s. Weil der Massenmittelpunkt in Ruhe bleibt, ist die von den Puffern maximal aufzunehmende Energie gleich der Summe der beiden kinetischen Energien, als gleich 64.3 kJ und 72.2 kJ. Davon übernehmen die Wagen den Teil, der sich bei den Puffern nicht nachweisen lässt:''W''<sub>Wagen</sub> = 64.3 kJ + 72.2 kJ - (63.4 kJ - 33.6 kJ) = 39.5 kJ. Dieser relativ grosse Anteil hängt mit Schlag zusammen, der entsteht, wenn der Ringfederpuffer auf Block geht. Dann rutscht die Ladung (Betonklötze) trotz massiver Befestigung ein wenig.
 '''[[Puffer-Prüfstand|Aufgabe]]'''