Sputnik

Sputnik

Sputnik 1 (russisch Спутник für Begleiter) ist von der Sowjetunion am 4. Oktober 1957 auf eine elliptische Umlaufbahn (Flughöhe zwischen 227 und 946 km über der Erdoberfläche) geschossen worden. Dieser erste künstliche Erdsatellit war zwar von der Sowjetunion für den Verlauf des Internationalen Geophysikalischen Jahres (IGY)(1957-58) angekündigt worden, doch rechnete die westliche Fachwelt erst Mitte 1958 mit der Fertigstellung der sowjetischen Entwicklungen. Der Start von Sputnik 1 machte aller Welt klar, dass die Sowjetunion nun in der Lage war, mit ihren Raketen nicht nur „den Weltraum“ zu erreichen, sondern auch jeden Punkt auf der Erde. Die faktische oder auch nur scheinbare Überlegenheit sowjetischen Interkontinentalraketen gegenüber jenen der USA löste in der westlichen Welt ein Gefühl der Bedrohung aus (Sputnik-Schock).

Im Sommersemester 2007 haben Studierende des Studienganges Aviatik die Hintergründe recherchiert und den Start mit Hilfe eines systemdynamischen Werkzeuges simuliert.

Aufgabenstellung

Die Flugbahn von Sputnik 1 soll mit Hilfe der verfügbaren Daten simuliert werden. Gestartet werde vom Äquator aus und die Umlaufbahn soll in die Äquatorialebene zu liegen kommen (zweidimensionale Bewegung). Das Modell ist auf eines erdfesten System zu beziehen.

Das Modell soll folgende Zusammenhänge möglichst korrekt abbilden:

• Impuls- und Massenbilanz
• Wirkung der Triebwerke
• Einfluss der Atmosphäre (Standardatmosphäre)
• Wirkung der Erde (Gravitations-, Zentrifugal- und Corioliskraft)

technische Daten

Trägerrakete R7

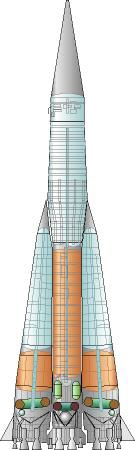
Die Trägerrakete besteht aus einem Bündel von 5 Einzelraketen, wobei die mittlere grösser ist, länger brennt und als zweite Stufe dient. Alle Triebwerke (5 x 4 Haupttriebwerke und 12 Steuertriebwerke wurden aus Sicherheitsgründen beim Start gleichzeitig gezündet.

1. Stufe:

Triebwerk	RD-107-8D74
Schub	4 x 790 kN
Startmasse	4 x 43'100 kg
Leermasse	4 x 3'500 kg
Brennzeit	120 s
spez. Impuls	2452 m/s (Meereshöhe)
spez. Impuls	3003 m/s (Vakuum)

2. Stufe:

Triebwerk	RD-108-8D75
Schub	1 x 745 kN
Startmasse	1 x 95'300 kg
Leermasse	1 x 7'500 kg
Brennzeit	330 s
spez. Impuls	2364 m/s (Meereshöhe)
spez. Impuls	3021 m/s (Vakuum)

Haupttriebwerk

Treibstoff	Kerosin
Oxidator	Sauerstoff
Mischungsverhältnis	1 : 2.47
Turbopumpe	4000 kW
Brennkammerdruck	58.50 bar
Düsenmündungsdruck	0.39 bar

Modellannahmen

Die Bilanzgleichungen bilden die zentralen Teile des Modells

• x-Impulsbilanz der ganzen Rakete
• y-Impulsbilanz der ganzen Rakete
• Massenbilanz 1. Stufe
• Massenbilanz 2. Stufe

Als weiter Zustandsgrössen (Bestandesgrösse, Stock) kommen noch die x- und die y-Koordinate dazu.

Impulsströme

Die Rakete tauscht auf drei Arten Impuls mit der Umgebung aus

• konvektiv, zusammen mit dem wegströmenden Gas
• leitungsartig mit der Luft (Luftwiderstand)
• quellenartig mit dem Gravitationsfeld

Im rotierenden Bezugssystem darf die Wirkung des (im Sinne von Albert Einstein verallgemeinerten) Gravitationsfeldes in drei Teile zerlegt werden

• Gravitationskraft der Erde
• Zentrifugalkraft
• Corioliskraft

Gravitations- und Zentrifugalkraft können zu einer verallgemeinerten Gravitationskraft zusammen gefasst werden. Die Corioliskraft steht immer senkrecht zur Geschwindigkeit der Rakete.

Luftwiderstand

In weniger als einer Minute ist die Rakete schneller als der Schall und die für die Kreisbahn notwendige Endgeschwindigkeit von 7900 m/s ist etwa zehn mal schneller als eine Kanonenkugel. Ein Widerstandsmodell, das den Unter- und Überschallbereich gut nachbildet, übersteigt die Möglichkeiten eines einführenden Kurses in die Physik der dynamischen Systeme. Der Fehler, der durch eine einfache Modellierung des Luftwiderstandes entsteht, wird aber infolge der abnehmende Dichte der Atmosphäre klein gehalten.

Der Luftwiderstand ist gleich kinetische Energiedichte der anströmenden Luft mal korrigierte Querschnittfläche

[math]F_W=\frac{\varrho}{2}v^2c_W A[/math]

wobei die Dichte der Luft (ρ) mit der Höhe abnimmt und der Widerstandsbeiwert (c_W) nur geschätzt werden kann.

Modell

SD-Modell