Potentiometer: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 16. November 2007, 04:57 Uhr

Funktionsweise

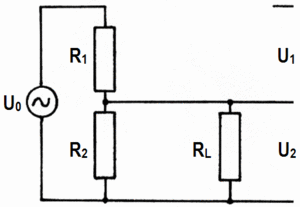
Ein Potentiometer (Potenziometer, kurz Poti) ist ein stetig einstellbarer Spannungsteiler. Es besteht aus einem Widerstandsdraht und einem beweglichen Gleitkontakt, der den Gesamtwiderstand elektrisch in zwei Teilwiderstände teilt. Je nach äußerer Beschaltung ergibt sich entweder ein linearer Widerstand, ein linearer Spannungsabgriff am zweiten Teilwiderstand oder mit einem Lastwiderstand ein belasteteter Spannungsteiler.

Potentiometer werden häufig zur Steuerung von elektrischen Geräten wie Lautstärkeeinstellung eines Radios oder Lichtregler (Dimmer) eingesetzt. Da Potentiometer durch den Abrieb am Schleifkontakt nicht verschleissfrei arbeiten und wegen der fortschreitenden Digitalisierung vieler elektronischer Funktionen werden sie zunehmend durch digitale Bedienelemente (z.B. Taster oder Inkrementalgeber) ersetzt.

unbelastet

Streng genommen versteht man unter einem unbelasteten Spannungsteiler eine Schaltung, bei welcher durch den Abgriff kein Strom fliessen kann, weil der Abgriff nicht verbunden ist. Dann wird die Ausgangsspannung (U₀) im Verhältnis der beiden Teilwiderstände (R₁ und R₂) geteilt. Ist der Lastwiderstand (R_L) viel grösser als die beiden Widerstände des Potentiometers (R₁ und R₂) spricht man immer noch von einem unbelasteten Spannungsteiler. Die Ausgangsspannung wird dann in guter Näherung im Verhältnis der beiden Teilwiderstände geteilt

[math]\frac {U_2}{U_0} = \frac {R_2}{R_1 + R_2}[/math] oder [math]U_2 = U_0 \frac {R_2}{R_1 + R_2}[/math]

belastet

Beim belasteten Potentiometer ist der Lastwiderstand von gleicher Grösse wie die beiden Teilwiderstände. Die Schaltung besteht dann aus zwei parallel betriebenen Widerstände (R₂ und R_L) die seriell mit einem dritten (R₁) verbunden sind. Folglich wird die Ausgangspannung nicht mehr im Verhältnis der beiden Teilwiderstände reduziert (geteilt)

[math]\frac{U_2}{U_0}=\frac {R_{2L}}{R_{tot}}=\frac{\frac {R_2 R_L}{R_2 + R_L}}{R_1+\frac {R_2 R_L}{R_2+R_L}}[/math]

oder

[math]U_2=U_0\frac{R_2}{R_1+R_2+\frac{R_1 R_2}{R_L}}=U_0\frac{R_2R_L}{R_1 R_2+R_1 R_L+R_2 R_L}[/math]

Energetisch arbeitet das Potentiometer ziemlich ungünstig. Vergleicht man das Verhältnis der über dem Lastwiderstand freigesetzten Leistung mit der von der Quelle gelieferten, erhält man

[math]\frac {P_2}{P_0}=\frac{U_2^2 (R_1 R_2+R_1 R_L+R_2R_L)}{U_0^2 R_L(R_2+R_L)}=\frac{(R_2)(R_2R_L)}{(R_2+R_L)(R_1 R_2+R_1 R_L+R_2 R_L)}[/math]

Die beiden Faktoren im Zähler sind kleiner als die zugehörigen Faktoren im Nenner.

@@ Zeile 8: / Zeile 8: @@
 Streng genommen versteht man unter einem unbelasteten Spannungsteiler eine Schaltung, bei welcher durch den Abgriff kein Strom fliessen kann, weil der Abgriff nicht verbunden ist. Dann wird die Ausgangsspannung (''U<sub>0</sub>'') im Verhältnis der beiden Teilwiderstände (''R<sub>1</sub>'' und ''R<sub>2</sub>'') geteilt. Ist der Lastwiderstand (''R<sub>L</sub>'') viel grösser als die beiden Widerstände des Potentiometers (''R<sub>1</sub>'' und ''R<sub>2</sub>'') spricht man immer noch von einem unbelasteten Spannungsteiler. Die Ausgangsspannung wird dann in guter Näherung im Verhältnis der beiden Teilwiderstände geteilt
-<math>\frac {U_2}{U_0} = \frac {R_2}{R_1 + R_2}</math> oder <math>U_2 = U_0 \frac {R_2}{R_1 + R_2}</math>
+:<math>\frac {U_2}{U_0} = \frac {R_2}{R_1 + R_2}</math> oder <math>U_2 = U_0 \frac {R_2}{R_1 + R_2}</math>
 ==belastet==
 Beim belasteten Potentiometer ist der Lastwiderstand von gleicher Grösse wie die beiden Teilwiderstände. Die Schaltung besteht dann aus zwei parallel betriebenen Widerstände (''R<sub>2</sub>'' und ''R<sub>L</sub>'') die seriell mit einem dritten (''R<sub>1</sub>'') verbunden sind. Folglich wird die Ausgangspannung nicht mehr im Verhältnis der beiden Teilwiderstände reduziert (geteilt)
-<math>\frac{U_2}{U_0}=\frac {R_{2L}}{R_{tot}}=\frac{\frac {R_2 R_L}{R_2 + R_L}}{R_1+\frac {R_2 R_L}{R_2+R_L}}</math>
+:<math>\frac{U_2}{U_0}=\frac {R_{2L}}{R_{tot}}=\frac{\frac {R_2 R_L}{R_2 + R_L}}{R_1+\frac {R_2 R_L}{R_2+R_L}}</math>
 oder
-<math>U_2=U_0\frac{R_2}{R_1+R_2+\frac{R_1 R_2}{R_L}}=U_0\frac{R_2R_L}{R_1 R_2+R_1 R_L+R_2 R_L}</math>
+:<math>U_2=U_0\frac{R_2}{R_1+R_2+\frac{R_1 R_2}{R_L}}=U_0\frac{R_2R_L}{R_1 R_2+R_1 R_L+R_2 R_L}</math>
 Energetisch arbeitet das Potentiometer ziemlich ungünstig. Vergleicht man das Verhältnis der über dem Lastwiderstand freigesetzten Leistung mit der von der Quelle gelieferten, erhält man
-<math>\frac {P_2}{P_0}=\frac{U_2^2 (R_1 R_2+R_1 R_L+R_2R_L)}{U_0^2 R_L(R_2+R_L)}=\frac{(R_2)(R_2R_L)}{(R_2+R_L)(R_1 R_2+R_1 R_L+R_2 R_L)}</math>
+:<math>\frac {P_2}{P_0}=\frac{U_2^2 (R_1 R_2+R_1 R_L+R_2R_L)}{U_0^2 R_L(R_2+R_L)}=\frac{(R_2)(R_2R_L)}{(R_2+R_L)(R_1 R_2+R_1 R_L+R_2 R_L)}</math>
 Die beiden Faktoren im Zähler sind kleiner als die zugehörigen Faktoren im Nenner.