Lösung zu Kraft auf Rohrstück: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
(Skizze und Detaillierung, Korrektur in 2. (- p_1 A_1 - p_2 A_2 )) |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:Kraft_auf_Rohrstueck.png]] |
|||
Bei dieser Problemstellung sollte man sowohl beim Aufstellen der [[Energiebilanz]] als auch der [[Impulsbilanz]] mit dem Überdruck ''p''<sub>e</sub> rechnen. |
|||
| ⚫ | |||
| ⚫ | |||
:liefert Zusammen mit der [[Kontinuitätsgleichung]] |
|||
| ⚫ | |||
:<math>v_1 A_1 = v_2 A_2</math> |
|||
| ⚫ | |||
:den Eintrittsdruck, wobei p<sub>2</sub> = p<sub>L</sub> = 10<sup>5</sup> Pa den Luftdruck und p<sub>e</sub> = p<sub>1</sub> - p<sub>2</sub> den Ueberdruck beim Eintritt darstellt |
|||
:den Druck beim Eintritt |
|||
:<math>p_1 = |
:<math>p_1 = p_2 + \frac {\rho}{2} \left(1 - \left(\frac {d_2}{d_1}\right)^4 \right) v_2^2</math> = p<sub>L</sub> + 46.9 kPa |
||
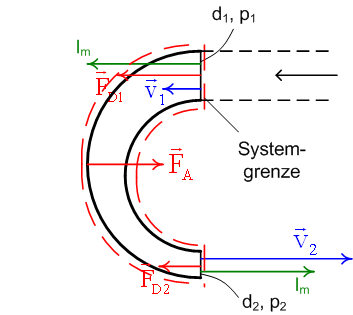
2. Die Impulsbilanz verlangt, dass sich die Festhaltekraft, die Überdruckkraft beim Eintritt und die beiden konvektiven Impulsströme zu Null addieren, weil der Impulsinhalt des Rohrstückes keine Änderung erfährt: |
2. Die [[Impulsbilanz]] verlangt, dass sich die Festhaltekraft, die Überdruckkraft beim Eintritt und die beiden konvektiven Impulsströme zu Null addieren, weil der Impulsinhalt des Rohrstückes keine Änderung erfährt: |
||
:<math> |
:<math>F_A - p_1 A_1 - p_2 A_2 + \left(- v_1 \right) \cdot I_m + v_2 \cdot \left( -I_m\right) = \dot p = 0</math> |
||
:<math>F_A = (p_e + p_L) A_1 + p_L A_2 + \left(v_1 + v_2\right) I_m = p_L (A_1 + A_2) + p_e A_1 + \rho v_2 \left(\left(\frac {d_2}{d_1}\right)^2 + 1 \right) I_V</math> = 982N + 368N + 49.1N + 196.3N = 1595 N |
|||
:Der [[Massenstrom]] <math>I_m = \rho I_V = \rho A v</math> hat eine Stärke von 19.63 kg/s. |
:Der [[Massenstrom]] <math>I_m = \rho I_V = \rho A v</math> hat eine Stärke von 19.63 kg/s. |
||
Version vom 4. März 2008, 19:04 Uhr
1. Die Energiebilanz, das Gesetz von Bernoulli, liefert zusammen mit der Kontinuitätsgleichung
- [math]p_1 + \frac {\rho}{2} v_1^2 = p_2 + \frac {\rho}{2} v_2^2, \quad v_1 A_1 = v_2 A_2, \quad v_1 = v_2 \cdot \frac {d_2^2}{d_1^2}[/math]
- den Eintrittsdruck, wobei p2 = pL = 105 Pa den Luftdruck und pe = p1 - p2 den Ueberdruck beim Eintritt darstellt
- [math]p_1 = p_2 + \frac {\rho}{2} \left(1 - \left(\frac {d_2}{d_1}\right)^4 \right) v_2^2[/math] = pL + 46.9 kPa
2. Die Impulsbilanz verlangt, dass sich die Festhaltekraft, die Überdruckkraft beim Eintritt und die beiden konvektiven Impulsströme zu Null addieren, weil der Impulsinhalt des Rohrstückes keine Änderung erfährt:
- [math]F_A - p_1 A_1 - p_2 A_2 + \left(- v_1 \right) \cdot I_m + v_2 \cdot \left( -I_m\right) = \dot p = 0[/math]
- [math]F_A = (p_e + p_L) A_1 + p_L A_2 + \left(v_1 + v_2\right) I_m = p_L (A_1 + A_2) + p_e A_1 + \rho v_2 \left(\left(\frac {d_2}{d_1}\right)^2 + 1 \right) I_V[/math] = 982N + 368N + 49.1N + 196.3N = 1595 N
- Der Massenstrom [math]I_m = \rho I_V = \rho A v[/math] hat eine Stärke von 19.63 kg/s.