Lösung zu zugeordneter Energiestrom Hydrodynamik: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Admin (Diskussion | Beiträge) KKeine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
#Die Stärke des [[zugeordneter Energiestrom|zugeordneten Energiestromes]] beträgt 62.25 kW. |
#Die Stärke des [[zugeordneter Energiestrom|zugeordneten Energiestromes]] beträgt 62.25 kW. |
||
#Damit bei einem Volumenstrom von 4.5 Litern pro Sekunde ein zugeordneter Energiestrom von 40 kW fliesst, muss der Druck 88.9 bar betragen. |
#Damit bei einem Volumenstrom von 4.5 Litern pro Sekunde ein zugeordneter Energiestrom von 40 kW fliesst, muss der Druck 88.9 bar betragen. |
||
#Weil der Druck linear in der Zeit abfällt und der Volumenstrom konstant bleibt, ist die transportierte Energie gleich der mittleren Leistung mal die Dauer, also gleich 30*10<sup>5</sup> Pa * 6*10<sup>-4</sup> |
#Weil der Druck linear in der Zeit abfällt und der Volumenstrom konstant bleibt, ist die transportierte Energie gleich der mittleren Leistung mal die Dauer, also gleich 30*10<sup>5</sup> Pa * 6*10<sup>-4</sup> m<sup>3</sup>/s * 300 s = 540 kJ. |
||
#Der [[Blasenspeicher]] gibt während den zehn Sekunden einen konstanten Volumenstrom von 1.2 l/s ab. Folglich geht das gespeicherte Volumen von 20 l auf 8 l und der Druck von 100 bar auf 29.4 bar zurück. Der zugeordnete Energiestrom sinkt in dieser Zeit von 12 kW auf 3.53 kW ab. Nimmt man das arithmetische Mittel dieser beiden Stromstärken und multipliziert diese mit der Zeit, erhält man eine Energieabnahme von 77.6 kJ. Den präzisen Wert für die Energieverminderung ermittelt man mit der exakten Formel für den [[Blasenspeicher]]<math>\Delta W = p_0V_0\ln \frac {V_0-V_a}{V_0-V_e}</math> = -62.2 kJ. Dass der exakte Wert kleiner als der gemittelte ist, hängt mit der konkaven Form der Druck-Volumen-Funktion zusammen. |
#Der [[Blasenspeicher]] gibt während den zehn Sekunden einen konstanten Volumenstrom von 1.2 l/s ab. Folglich geht das gespeicherte Volumen von 20 l auf 8 l und der Druck von 100 bar auf 29.4 bar zurück. Der zugeordnete Energiestrom sinkt in dieser Zeit von 12 kW auf 3.53 kW ab. Nimmt man das arithmetische Mittel dieser beiden Stromstärken und multipliziert diese mit der Zeit, erhält man eine Energieabnahme von 77.6 kJ. Den präzisen Wert für die Energieverminderung ermittelt man mit der exakten Formel für den [[Blasenspeicher]]<math>\Delta W = p_0V_0\ln \frac {V_0-V_a}{V_0-V_e}</math> = -62.2 kJ. Dass der exakte Wert kleiner als der gemittelte ist, hängt mit der konkaven Form der Druck-Volumen-Funktion zusammen. |
||
Version vom 5. Oktober 2008, 07:08 Uhr
- Die Stärke des zugeordneten Energiestromes beträgt 62.25 kW.
- Damit bei einem Volumenstrom von 4.5 Litern pro Sekunde ein zugeordneter Energiestrom von 40 kW fliesst, muss der Druck 88.9 bar betragen.
- Weil der Druck linear in der Zeit abfällt und der Volumenstrom konstant bleibt, ist die transportierte Energie gleich der mittleren Leistung mal die Dauer, also gleich 30*105 Pa * 6*10-4 m3/s * 300 s = 540 kJ.
- Der Blasenspeicher gibt während den zehn Sekunden einen konstanten Volumenstrom von 1.2 l/s ab. Folglich geht das gespeicherte Volumen von 20 l auf 8 l und der Druck von 100 bar auf 29.4 bar zurück. Der zugeordnete Energiestrom sinkt in dieser Zeit von 12 kW auf 3.53 kW ab. Nimmt man das arithmetische Mittel dieser beiden Stromstärken und multipliziert diese mit der Zeit, erhält man eine Energieabnahme von 77.6 kJ. Den präzisen Wert für die Energieverminderung ermittelt man mit der exakten Formel für den Blasenspeicher[math]\Delta W = p_0V_0\ln \frac {V_0-V_a}{V_0-V_e}[/math] = -62.2 kJ. Dass der exakte Wert kleiner als der gemittelte ist, hängt mit der konkaven Form der Druck-Volumen-Funktion zusammen.
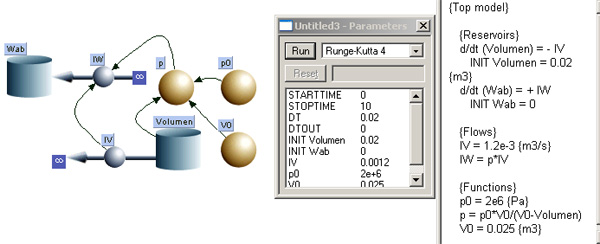
Die letzte Aufgabe kann mit Hilfe eines systemdynamischen Modells effizient gelöst werden. Untenstehend das Systemdiagramm, die Parameter und die Gleichungen.