Lösung zu Widerstand einer Glühbirne: Unterschied zwischen den Versionen
Inhalt hinzugefügt Inhalt gelöscht
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 22: | Zeile 22: | ||
#Die Leistung ist gleich Spannung über dem Draht mal Stromstärke durch den Draht <math>P=UI=\frac{U^2}{R}</math> = 16.1 W, 46.5 W, 78.4 W. |
#Die Leistung ist gleich Spannung über dem Draht mal Stromstärke durch den Draht <math>P=UI=\frac{U^2}{R}</math> = 16.1 W, 46.5 W, 78.4 W. |
||
#Der kleinstmögliche Widerstand von etwa 0.15 Ω entspricht dem Kaltwiderstand R<sub>20</sub>. Nun verwenden wir für den Widerstand die quadratische Gleichung mit der Temperaturerhöhung. Diese lösen wir nach der Temperaturerhöhung auf und erhalten dann 3 Werte für die Temperaturerhöhung: ''Δ T'' = 1641°C, 2156°C und 2430°C. Die gesuchten Drahttemperaturen betragen also 1661°C, 2176°C und 2450°C. |
#Der kleinstmögliche Widerstand von etwa 0.15 Ω entspricht dem Kaltwiderstand R<sub>20</sub>. Nun verwenden wir für den Widerstand die quadratische Gleichung mit der Temperaturerhöhung. Diese lösen wir nach der Temperaturerhöhung auf und erhalten dann 3 Werte für die Temperaturerhöhung: ''Δ T'' = 1641°C, 2156°C und 2430°C. Die gesuchten Drahttemperaturen betragen also 1661°C, 2176°C und 2450°C. |
||
#Das Diagramm zeigt die 3 Werte nicht auf einer Geraden sondern auf einer leicht gekrümmten Kurve. Zu dieser Abweichung können verschiedene Effekte beitragen: Wärmeverluste durch Wärmeleitung über die Anschlussdrähte, Spannungsverlust bei den Anschlussdrähten, Konvektionsverluste an das Gas im Lampenkolben, ... |
|||
#Das Daigramm mit |
|||
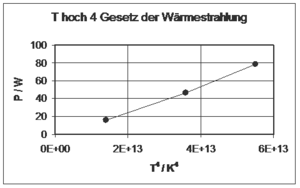
[[Bild:Thoch4_Gesetz.png|thumb|Glühbirne: Leistung gegen T<sup>4</sup>]] |
|||
[[Bild:Thoch4_Gesetz.png|thumb|R-U-Kennlinie]] Die Graphik zeigt die Widerstands-Spannungs-Kennlinie einer Glühbirne. |
|||
Zum Lösen von quadratischen Gleichungen: Zuerst bringt man die gegebene Gleichung in Normalform: <math>ax^2+bx+c=0</math>. Dann berechnet man die 2 möglichen Lösungen mit folgender Formel: <math>x_{1,2} = (-b \pm \sqrt {b^2-4ac})/(2a)</math> und wählt dann daraus die physikalisch sinnvolle Lösung aus (hier ist es die positive Lösung, weil eine negative Temperaturerhöhung hier keinen Sinn ergibt). |
Zum Lösen von quadratischen Gleichungen: Zuerst bringt man die gegebene Gleichung in Normalform: <math>ax^2+bx+c=0</math>. Dann berechnet man die 2 möglichen Lösungen mit folgender Formel: <math>x_{1,2} = (-b \pm \sqrt {b^2-4ac})/(2a)</math> und wählt dann daraus die physikalisch sinnvolle Lösung aus (hier ist es die positive Lösung, weil eine negative Temperaturerhöhung hier keinen Sinn ergibt). |
||
Version vom 2. November 2008, 07:48 Uhr
Die zu den Spannungswerten benötigten Widerstandswerte liest man aus dem Diagramm R-U-Charakteristik ab:
| 0 V | 0.15 Ω |
| 5 V | 1.55 Ω |
| 10 V | 2.15 Ω |
| 12 V | 2.35 Ω |
| 14 V | 2.50 Ω |
- Die Stromstärke ist gleich Spannung durch Widerstand [math]I=\frac{U}{R}[/math] = 5.1 A.
- Die Leistung ist gleich Spannung über dem Draht mal Stromstärke durch den Draht [math]P=UI=\frac{U^2}{R}[/math] = 16.1 W, 46.5 W, 78.4 W.
- Der kleinstmögliche Widerstand von etwa 0.15 Ω entspricht dem Kaltwiderstand R20. Nun verwenden wir für den Widerstand die quadratische Gleichung mit der Temperaturerhöhung. Diese lösen wir nach der Temperaturerhöhung auf und erhalten dann 3 Werte für die Temperaturerhöhung: Δ T = 1641°C, 2156°C und 2430°C. Die gesuchten Drahttemperaturen betragen also 1661°C, 2176°C und 2450°C.
- Das Diagramm zeigt die 3 Werte nicht auf einer Geraden sondern auf einer leicht gekrümmten Kurve. Zu dieser Abweichung können verschiedene Effekte beitragen: Wärmeverluste durch Wärmeleitung über die Anschlussdrähte, Spannungsverlust bei den Anschlussdrähten, Konvektionsverluste an das Gas im Lampenkolben, ...
Zum Lösen von quadratischen Gleichungen: Zuerst bringt man die gegebene Gleichung in Normalform: [math]ax^2+bx+c=0[/math]. Dann berechnet man die 2 möglichen Lösungen mit folgender Formel: [math]x_{1,2} = (-b \pm \sqrt {b^2-4ac})/(2a)[/math] und wählt dann daraus die physikalisch sinnvolle Lösung aus (hier ist es die positive Lösung, weil eine negative Temperaturerhöhung hier keinen Sinn ergibt).