Lösung zu Aviatik 2008/Ass: Unterschied zwischen den Versionen

Aus SystemPhysik
Inhalt hinzugefügt Inhalt gelöscht
Zeile 25: Zeile 25:


==Aufgabe 4==
==Aufgabe 4==
#Massenstromstärke: <math>I_m=\varrho I_V=\varrho v_1 A</math> = 201 kg/s. Nun ist die [[Schubkraft]] gleich Geschwindigkeitsdifferenz mal die Massenstromstärke. Daraus folgt <math>v_2=\frac{F_S}{I_m}+v_1</math> = 499 m/s.
#Die [[Prozessleistung]] ist gleich der Differenz der Energieströme <math>P=I_{W2}-I_{W1}=\frac 12\left(v_2^2-v_1^2\right)I_m</math> = 18.74 MW.
#Die Schubkraft setzt sich nun aus zwei Teilen zusammen <math>F_S=0.2\left(2v_2-v_1\right)I_m+0.8\left(v_2-v_1\right)I_m</math>. Daraus folgt <math>v_2=\frac 56\left(\frac{F_S}{I_m}+v_1\right)</math> = 416 m/s.
#Die Leistung setzt sich nun auch aus zwei Teilen zusammen <math>P=\frac 12\left(0.2(2v_2)^2+0.8v_2^2-v_1^2\right)I_m</math> = 21.5 MW.


==Aufgabe 5==
==Aufgabe 5==

Version vom 20. August 2009, 11:58 Uhr

Aufgabe 1

Die Spannung über Kondensator und Widerstand sinkt exponentiell mit der Zeit ab. Mit der Zeitkonstanten [math]\tau=RC[/math] = 0.6 s folgt [math]U=U_0e^{-t/\tau}[/math] = 0.944 V.

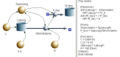
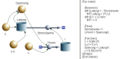
Die Bilder zeigen die Systemdiagramme sowie die Gleichungen.

  • RC-Glied

    RC-Glied

  • LC-Glied

    LC-Glied

Aufgabe 2

  1. Zum Zeitpunkt 0.8 s beträgt die Beschleunigung des Wagens B 2 m/s2 (1.96 m/s2) entsprechend der Steigung der Kurve im v-t-Diagramm. Folglich ist die Reibkraft gleich 80 kN (78.5 kN).
  2. Der Wagen B verschiebt sich um 2.1 m (Fläche unter der Kurve im v-t-Diagramm).
  3. Während sich der Puffer zusammen zieht, werden 77 kNs Impuls übertragen. Die Masse des auflaufenden Wagens beträgt damit [math]m=\frac{\Delta p}{\Delta v}[/math] = 60 t.
  4. Der Wagen verschiebt sich um 0.5 m (0.509 m). Damit ist die dissipierte Energie (Reibkraft mal Verschiebung) gleich 40 kJ (39.95 kJ).

Die in Klammern gesetzten Werte sind der Simulation entnommmen.

Aufgabe 3

  1. Im Bezugssystem Waschküche wirken zwei Kräfte auf das Fünffrankenstück ein, die Gewichtskraft und die Normalkraft. Beide Kräfte wirken nach unten und erteilen dem Geldstück die notwendige Beschleunigung.
  2. Der Beschleunigungsvektor zeigt gegen die Mitte der Trommel. Sein Betrag ist gleich [math]a=\omega^2r[/math] = 4299 m/s2 (ω = 146.6 1/s).
  3. Am höchsten und am tiefsten Punkt der Bahn erzeugen Gewichts- und Normalkraft die Beschleunigung:
höchster Punkt: [math]F_G+F_N=ma[/math] daraus folgt: [math]F_N=\left(\frac ag-1\right)F_G[/math] = 437 mal die Gewichtskraft
tiefster Punkt: [math]-F_G+F_N=ma[/math] daraus folgt: [math]F_N=\left(\frac ag+1\right)F_G[/math] = 439 mal die Gewichtskraft

Aufgabe 4

  1. Massenstromstärke: [math]I_m=\varrho I_V=\varrho v_1 A[/math] = 201 kg/s. Nun ist die Schubkraft gleich Geschwindigkeitsdifferenz mal die Massenstromstärke. Daraus folgt [math]v_2=\frac{F_S}{I_m}+v_1[/math] = 499 m/s.
  2. Die Prozessleistung ist gleich der Differenz der Energieströme [math]P=I_{W2}-I_{W1}=\frac 12\left(v_2^2-v_1^2\right)I_m[/math] = 18.74 MW.
  3. Die Schubkraft setzt sich nun aus zwei Teilen zusammen [math]F_S=0.2\left(2v_2-v_1\right)I_m+0.8\left(v_2-v_1\right)I_m[/math]. Daraus folgt [math]v_2=\frac 56\left(\frac{F_S}{I_m}+v_1\right)[/math] = 416 m/s.
  4. Die Leistung setzt sich nun auch aus zwei Teilen zusammen [math]P=\frac 12\left(0.2(2v_2)^2+0.8v_2^2-v_1^2\right)I_m[/math] = 21.5 MW.

Aufgabe 5

Aufgabe 6

Aufgabe 7

Aufgabe 8

Aufgabe

Abgerufen von „http://systemdesign.ch/index.php?title=Lösung_zu_Aviatik_2008/Ass&oldid=9197“