Lösung zu Abfüllwaage: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 2: | Zeile 2: | ||
===ohne Loch im Becherglas=== |
===1. ohne Loch im Becherglas=== |
||
Die Impulsbilanz bezüglich des Systems Becherglas lautet (positive Richtung nach unten) |
Die Impulsbilanz bezüglich des Systems Becherglas lautet (positive Richtung nach unten) |
||
| Zeile 13: | Zeile 13: | ||
Die Geschwindigkeiten beim Ausfluss ''v''<sub>1</sub> und beim Auftreffen auf die Wasseroberfläche ''v''<sub>2</sub> ergeben sich aus der Energiebilanz ([[Ausflussgesetz von Torricelli|Torricelli]]) |
Die Geschwindigkeiten beim Ausfluss ''v''<sub>1</sub> und beim Auftreffen auf die Wasseroberfläche ''v''<sub>2</sub> ergeben sich aus der Energiebilanz ([[Ausflussgesetz von Torricelli|Torricelli]]) |
||
:<math> v_1 = \sqrt{2gh_1}, \quad v_2 = \sqrt{2gh_2}</math> |
:<math> v_1 = \sqrt{2gh_1} = 4.43 m/s, \quad v_2 = \sqrt{2gh_2} = 5.24 m/s</math> |
||
also gilt für den konvektiven Impulsstrom |
also gilt für den konvektiven Impulsstrom |
||
:<math>I_{p1} = 2 g \rho A_1 \sqrt{h_1 h_2}</math> = 7.29 N |
:<math>I_{p1} = 2 g \rho A_1 \sqrt{h_1 h_2}</math> = 7.29 N, A<sub>1</sub> = 0.000'314 m<sup>2</sup> |
||
Bei einer |
Bei einer totalen Masse von 2 kg + 1000 kg/m<sup>3</sup> * 0.2 m * π/4 * (0.1 m)<sup>2</sup> = 3.57 kg und einer Gewichtskraft von 35.0 N hat die Normalkraft (entspricht der Waagenanzeige) einen momentanen Wert von |
||
:<math>F_N = F_G + I_{p1}</math> = 42.3 N |
:<math>F_N = F_G + I_{p1}</math> = 42.3 N |
||
===mit Loch im Becherglas=== |
===2. mit Loch im Becherglas=== |
||
Die Volumenströme I<sub>V1</sub> und I<sub>V2</sub> durch die beiden Ausflusslöcher sind gleich gross, weil der Wasserspiegel im Becherglas auf konstanter Höhe bleibt. Die Geschwindigkeit v<sub>3</sub> im Loch des Becherglases beträgt: <math> v_3 = \sqrt{2gh_3}</math>. Daraus kann man die Stärke des zweiten konvektiven Impulsstromes im Boden des Becherglases berechnen: |
Die Volumenströme I<sub>V1</sub> und I<sub>V2</sub> durch die beiden Ausflusslöcher sind gleich gross, weil der Wasserspiegel im Becherglas auf konstanter Höhe bleibt. Die Geschwindigkeit v<sub>3</sub> im Loch des Becherglases beträgt: <math> v_3 = \sqrt{2gh_3}</math>. Daraus kann man die Stärke des zweiten konvektiven Impulsstromes im Boden des Becherglases berechnen: |
||
Version vom 23. Februar 2010, 09:13 Uhr
1. ohne Loch im Becherglas
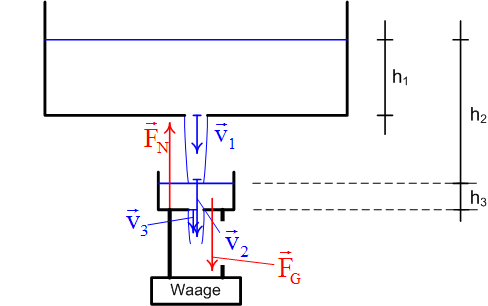
Die Impulsbilanz bezüglich des Systems Becherglas lautet (positive Richtung nach unten)
- [math]{-}F_N + F_G + I_{p1} = 0[/math]
Die Stärke des konvektiven Impulsstromes Ip1 ist gleich
- [math]I_{p1} = \rho v_2 I_{V1} = \rho v_2 v_1 A_1 [/math]
Die Geschwindigkeiten beim Ausfluss v1 und beim Auftreffen auf die Wasseroberfläche v2 ergeben sich aus der Energiebilanz (Torricelli)
- [math] v_1 = \sqrt{2gh_1} = 4.43 m/s, \quad v_2 = \sqrt{2gh_2} = 5.24 m/s[/math]
also gilt für den konvektiven Impulsstrom
- [math]I_{p1} = 2 g \rho A_1 \sqrt{h_1 h_2}[/math] = 7.29 N, A1 = 0.000'314 m2
Bei einer totalen Masse von 2 kg + 1000 kg/m3 * 0.2 m * π/4 * (0.1 m)2 = 3.57 kg und einer Gewichtskraft von 35.0 N hat die Normalkraft (entspricht der Waagenanzeige) einen momentanen Wert von
- [math]F_N = F_G + I_{p1}[/math] = 42.3 N
2. mit Loch im Becherglas
Die Volumenströme IV1 und IV2 durch die beiden Ausflusslöcher sind gleich gross, weil der Wasserspiegel im Becherglas auf konstanter Höhe bleibt. Die Geschwindigkeit v3 im Loch des Becherglases beträgt: [math] v_3 = \sqrt{2gh_3}[/math]. Daraus kann man die Stärke des zweiten konvektiven Impulsstromes im Boden des Becherglases berechnen:
- [math]I_{p2} = \rho v_3 I_{V2} = \rho \sqrt{2gh_3} I_{V1} = 2 \rho g \sqrt{h_3 h_1} A_1[/math] = 2.8 N
Aus der Impulsbilanz [math]{-}F_N + F_G + I_{p1} - I_{p2} = 0[/math] erhält man wieder die Festhaltekraft (oder Normalkraft)
- [math]F_N = F_G + I_{p1} - I_{p2}[/math] = 39.5 N