Lösung zu Kreisprozess mit Helium: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Version vom 11. April 2010, 15:23 Uhr

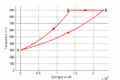
T-S-Diagramm
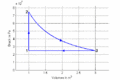
p-V-Diagramm

Im T-S-Diagramme verläuft die isochore Zustandsänderung exponentiell nach oben, die isotherme horizontal und die isobare wiederum exponentiell und weniger steil zurück zum Ausgangspunkt. Im p-V-Diagramm steigt die Kurve zuerst vertikal nach oben, läuft dann auf einer Hyperbel ([math]pV=p_0V_0[/math]) nach rechts unten und zum Schluss auf einer Horizontalen nach links. Im T-S-Diagramm entspricht die Fläche unter der Kurve eines Teilprozesses der Wärme. Im p-V-Diagramm ergibt die entsprechende Fläche die (negativ genommene) Arbeit.
Das universelle Gasgesetz liefert für den unteren Druck einen Wert von p₁ = n * R * T₁ / V₁ = 10 kmol * 8.31 J/K/mol * 300 K / 1 m³ = 249 bar. Der Druck nach dem Aufheizen (1. Teilprozess) beträgt p₂ = n * R * T₂ / V₂ = 10 kmol * 8.31 J/K/mol * 900 K / 1 m³ = 748 bar. Das Volumen beträgt nach dem zweiten, isothermen Teilprozess V₃ = p₂ / p₃ * V₂ = 748 bar / 249 bar * 1 m³ = 3 m³.
Im ersten Teilprozess nimmt die Entropie um [math]\Delta S_{12}=n\hat c_V\ln{\frac{T_2}{T_1}}=\frac 3 2 nR\ln{\frac{T_2}{T_1}}[/math] = 1.5 * 10 kmol * 8.31 J/K/mol * ln(900 K / 300 K) = 137 kJ/K zu. Im dritten, isobaren Teilprozess nimmt die Entropie um 5/3 dieses Wertes, also um 228 kJ/K ab, weil die Wärmekapazität bei konstantem Druck 5/3 der Wärmekapazität bei konstantem Volumen ist. Die Differenz von 91 kJ/K muss im zweiten, isothermen Teilprozess aus einem Wärmebad zugeführt werden.
Im ersten Teilprozess nimmt die innere Energie des Heliums um [math]W_{therm12}=\Delta W=\frac{3}{2}nR\Delta T[/math] = 1.5 * 10 kmol * 8.31 J/K/mol * 600 K = 74.8 MJ zu. Bei der nachfolgenden isothermen Zustandsänderung muss dem Gas zusätzliche Energie in Form von Wärme zugeführte werden [math]W_{therm23}=T_2 \Delta S_{23} =T_2 n R \ln{\frac{V_3}{V_2}}[/math] = 900 K * 10 kmol * 8.31 J/K/mol * ln(3 m3 / 1 m3) = 82.2 MJ (bei einer isothermen Expansion bleibt die Entropie, welche die Energie trägt, im Gas drin; die Energie geht dagegen direkt in Form von Arbeit weg). Um die Energie für diese beiden Teilprozesse aus dem Ofen abzutransportieren, muss der Ofen die folgende Entropiemenge abgeben [math]S_{Ofen}=\frac{W_{therm13}}{T_{Ofen}}=\frac{157 MJ}{1000 K}[/math] = 157 kJ/K. Im dritten Teilprozess, dem isobaren, wird die eine bestimmte Energiemenge in Form von Wärme abgeführt [math]W_{therm31}=\frac 5 2 nR \Delta T[/math] = 125 MJ. Diese Energie muss bei einer Temperatur von 280 K von der Entropie [math]S_{Um}=\frac{W_{therm31}}{T_{Um}}[/math] = 445 kJ/K in die Umwelt hinein getragen werden. Erzeugt wird die Differenz zwischen der von Umwelt aufgenommenen und der vom Ofen abgegebenen Entropie. Diese Differenz beträgt 288 kJ/K.

Aufgabe

@@ Zeile 6: / Zeile 6: @@
 #Das [[ideales Gas|universelle Gasgesetz]] liefert für den unteren Druck einen Wert von p<sub>1</sub> = n * R * T<sub>1</sub> / V<sub>1</sub> = 10 kmol * 8.31 J/K/mol * 300 K / 1 m<sup>3</sup> = 249 bar. Der Druck nach dem Aufheizen (1. Teilprozess) beträgt p<sub>2</sub> = n * R * T<sub>2</sub> / V<sub>2</sub> = 10 kmol * 8.31 J/K/mol * 900 K / 1 m<sup>3</sup> = 748 bar. Das Volumen beträgt nach dem zweiten, isothermen Teilprozess V<sub>3</sub> = p<sub>2</sub> / p<sub>3</sub> * V<sub>2</sub> = 748 bar / 249 bar * 1 m<sup>3</sup> = 3 m<sup>3</sup>.
 #Im ersten Teilprozess nimmt die Entropie um <math>\Delta S_{12}=n\hat c_V\ln{\frac{T_2}{T_1}}=\frac 3 2 nR\ln{\frac{T_2}{T_1}}</math> = 1.5 * 10 kmol * 8.31 J/K/mol * ln(900 K / 300 K) = 137 kJ/K zu. Im dritten, isobaren Teilprozess nimmt die Entropie um 5/3 dieses Wertes, also um 228 kJ/K ab, weil die Wärmekapazität bei konstantem Druck 5/3 der Wärmekapazität bei konstantem Volumen ist. Die Differenz von 91 kJ/K muss im zweiten, isothermen Teilprozess aus einem Wärmebad zugeführt werden.
-#Im ersten Teilprozess nimmt die innere Energie des Heliums um <math>W_{therm12}=\Delta W=\frac{3}{2}nR\Delta T</math> = 1.5 * 10 kmol * 8.31 J/K/mol * 600 K = 74.8 MJ zu. Bei der nachfolgenden isothermen Zustandsänderung muss dem Gas zusätzliche Energie in Form von Wärme zugeführte werden <math>W_{therm23}=T_2 \Delta S_{23} =T_2 n R \ln{\frac{V_2}{V_3}}</math> = 900 K * 10 kmol * 8.31 J/K/mol * ln(3 m3 / 1 m3) = 82.2 MJ (bei einer isothermen Expansion bleibt die Entropie, welche die Energie trägt, im Gas drin; die Energie geht dagegen direkt in Form von Arbeit weg). Um die Energie für diese beiden Teilprozesse aus dem Ofen abzutransportieren, muss der Ofen die folgende Entropiemenge abgeben <math>S_{Ofen}=\frac{W_{therm13}}{T_{Ofen}}=\frac{157 MJ}{1000 K}</math> = 157 kJ/K. Im dritten Teilprozess, dem isobaren, wird die eine bestimmte Energiemenge in Form von Wärme abgeführt <math>W_{therm31}=\frac 5 2 nR \Delta T</math> = 125 MJ. Diese Energie muss bei einer Temperatur von 280 K von der Entropie <math>S_{Um}=\frac{W_{therm31}}{T_{Um}}</math> = 445 kJ/K in die Umwelt hinein getragen werden. Erzeugt wird die Differenz zwischen der von Umwelt aufgenommenen und der vom Ofen abgegebenen Entropie. Diese Differenz beträgt 288 kJ/K.
+#Im ersten Teilprozess nimmt die innere Energie des Heliums um <math>W_{therm12}=\Delta W=\frac{3}{2}nR\Delta T</math> = 1.5 * 10 kmol * 8.31 J/K/mol * 600 K = 74.8 MJ zu. Bei der nachfolgenden isothermen Zustandsänderung muss dem Gas zusätzliche Energie in Form von Wärme zugeführte werden <math>W_{therm23}=T_2 \Delta S_{23} =T_2 n R \ln{\frac{V_3}{V_2}}</math> = 900 K * 10 kmol * 8.31 J/K/mol * ln(3 m3 / 1 m3) = 82.2 MJ (bei einer isothermen Expansion bleibt die Entropie, welche die Energie trägt, im Gas drin; die Energie geht dagegen direkt in Form von Arbeit weg). Um die Energie für diese beiden Teilprozesse aus dem Ofen abzutransportieren, muss der Ofen die folgende Entropiemenge abgeben <math>S_{Ofen}=\frac{W_{therm13}}{T_{Ofen}}=\frac{157 MJ}{1000 K}</math> = 157 kJ/K. Im dritten Teilprozess, dem isobaren, wird die eine bestimmte Energiemenge in Form von Wärme abgeführt <math>W_{therm31}=\frac 5 2 nR \Delta T</math> = 125 MJ. Diese Energie muss bei einer Temperatur von 280 K von der Entropie <math>S_{Um}=\frac{W_{therm31}}{T_{Um}}</math> = 445 kJ/K in die Umwelt hinein getragen werden. Erzeugt wird die Differenz zwischen der von Umwelt aufgenommenen und der vom Ofen abgegebenen Entropie. Diese Differenz beträgt 288 kJ/K.
 '''[[Kreisprozess mit Helium|Aufgabe]]'''