Lösung zu Fadenspule

1.

Schnittbild der Fadenspule

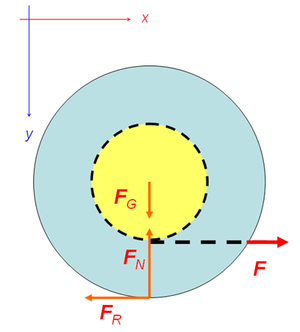
Auf die Fadenspule wirkt neben dem Faden nur noch das Gravitationsfeld (Gewichtskraft) und die Unterlage (Normalkraft und Reibungskraft) ein.

2. Ein Teil des mit dem Faden zugeführten x-Impuls bleibt in der Spule, der Rest geht an die Unterlage (Haftreibung) weg. Der vom Graviationsfeld zufliessende y-Impuls (Gewichtskraft) geht unmittelbar an die Unterlage (Normalkraft) weg. Der x-Impuls, der in der Fadenspule in y-Richtung fliessen muss, erzeugt Quellen und Senken des z-Drehimpulses (der in der Fadenspule verbleibende x-Impuls wird im räumlichen Mittel im Massenmittelpunkt gespeichert. Diese Überlegungen bilden den Kern der Impuls- und Drehimpulsbilanzen

x-Impuls: [math]F - F_R = \dot p_x = m \dot v_x[/math]

y-Impuls: [math]F_G - F_N = \dot p_y = 0[/math]

z-Drehimpuls: [math]F_R R - F r = \dot L_z = J \dot \omega_y[/math]

3. In der Rollphase gillt die Rollbedingung [math]v_x = \omega R[/math], in der Gleitphase das Gleitreibungsgesetz [math]F_R = \mu F_N[/math]

4. Die Rolle beginnt zu rutschen, sobald die Haftreibungskraft die Haftreibungsgrenze (maximale Haftreibungskraft) erreicht hat. Die maximale Haftreibungskraft ist in der Regel etwas grösser als die Gleitreibungskraft, was hier vernachlässigt wird. Beim Übergang von der Roll- in die Rutschphase gelten sowohl die Rollbedingung als auch das Gleitreibungsgesetz. Aus diesen insgesamt fünf Gleichungen lässt sich die kritische Seilkraft berechnen

x-Impuls: [math]F - F_R = m \dot v[/math]

y-Impuls: [math]F_G - F_N = 0[/math]

z-Drehimpuls: [math]F_R R - F r = J \dot \omega[/math]

Rollbedingung: [math]v = \omega R[/math] oder [math]\dot v = \dot \omega R[/math]

Gleitreibungsgesetz: [math]F_R = \mu F_N[/math]