Rohrreibungszahl

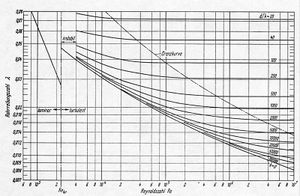
Die Rohrreibungszahl dient in erster Linie der quantitativen Beschreibung des Rohrreibung bei turbulenter Strömung. Der Druckabfall über dem Rohrstück steigt dann quadratisch zur Volumenstromstärke an

[math]\Delta p = kI_V^2[/math]

Der Faktor k ist proportional zur Dichte des strömenden Mediums und zur Länge des Rohres. Zudem nimmt er mit dem Durchmesser hoch fünf ab

[math]k=\zeta \frac {\rho} {2A^2}=\lambda \frac {8 \rho l}{\pi^2d^5}[/math]

Die dimensionslose Grösse λ (lambda) heisst Rohrreibungszahl. Die Rohrreibungszahl selber ändert sich mit der Volumenstromstärke. Um diese Abhängigkeit losgelöst vom konkreten Medium beschreiben zu können, gibt man die Rohrreibungszahl in Funktion der ebenfalls dimensionslosen Reynolds-Zahl Re an.

Im laminaren Bereich steigt der Druck linear mit dem Volumenstrom

[math]\Delta p=R_V I_V[/math]

wobei für den Strömungswiderstand gilt

[math]R_V=\frac{128\eta l}{\pi d^4}[/math]

Rein algebraisch lässt sich das laminare Strömungsgesetz ins turbulente umschreiben, in der Strömungswiderstand umgeschrieben wird

[math]\Delta p=R_V I_V=\frac{R_V}{I_V}I_V^2[/math]