Lösung zu Badewanne auf Rutsche
Beschleunigung der Wanne
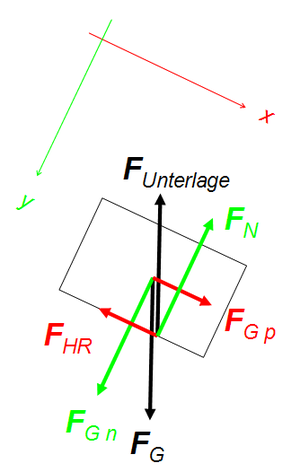
Die Badewanne kann, falls man die Relativbewegung des Wasser vernachlässigt, als Klotz angesehen werden, der auf einer schiefen Ebene nach unten gleitet. Obwohl die Lösung dieses Problems praktisch in jeder Formelsammlung steht, soll sie hier nochmals hergeleitet werden. Wir folgen dabei der Lösungsmethode der Ingenieure:
- Freischneiden: in einem ersten Schritt zeichnet man alle Körper einzeln auf und gibt für jeden Körper alle Kräfte an, die auf ihn einwirken. Auf die Badewanne wirken eigentlich nur zwei Kräfte ein, die Gewichtskraft und die Unterlagskraft. Die Skizze zeigt die beiden Kräfte auf den ruhenden Körper. Beide Kräfte (Vektoren) dürfen nun in je zwei Komponenten zerlegt werden. Die beiden Komponenten der Unterlagskraft heissen Normalkraft und Reibungskraft (Haftreibung beim ruhenden Körper und Gleitreibung beim bewegten). Die parallel zur schiefen Ebene gerichtete Komponente der Gewichtskraft nennt man auch Hangabtriebskraft. Dieser Name ist nicht falsch, aber eigentlich überflüssig. Dass die Normalkomponente der Gewichtskraft oft Normalkraft genannt wird, ist ein eher düsteres Kapitel der Schulphyisik. Beim gleitenden Körper ist die Gleitreibung kleiner als die Parallelkomponente der Gewichtskraft.
- Nun führt man ein der Situation angepasstes Koordinatensystem ein. Mit der Zerlegung der Kräfte hat man die Achsen des Koordinatensystems bis auf die Orientierung eigentlich schon festgelegt. Die Unterlagskraft kann dann die Gewichtskraft nicht mehr vollständig kompensieren.
- Nun formuliert man die Impulsbilanz oder das Grundgesetz der für beide Koordinatenrichtungen
- [math]F_G\sin\alpha-F_R=ma_B[/math]
- [math]F_G\cos\alpha-F_N=0[/math]
Aus der Gleichgewichtsbedingung in y-Richtung folgt, dass die Normalkraft gleich der Normalkomponente der Gewichtskraft ist
- [math]F_N=F_G\cos\alpha[/math]
Diese Formel gilt nur im einfachsten Spezialfall und sollte nicht dazu benutzt werden, die Normalkomponente der Gewichtskraft als Normalkraft zu bezeichnen. Mit Hilfe des Gleitreibungsgesetzes [math]F_R=\mu F_N[/math] und des Gravitationsgesetzes [math]F_G=mg[/math] lässt sich die Impulsbilanz in x-Richtung nach der Beschleunigung auflösen
- [math]a=g(\sin\alpha-\mu\cos\alpha)[/math]
Ohne Reibung wäre die Beschleunigung der Wanne gleich der Parallelkomponente der Gravitaionsfeldstärke. Im konkreten Fall beträgt die Beschleunigung 1.5 m/s2.
Neigung der Wasseroberläche
Im Ruhezustand verläuft die Wasseroberfläche normal zur lokal nachweisbaren Gravitationsfeldstärke. Das Gravitationsfeld in einem zweiten Bezugssystem erhält man durch Überlagerung (Superposition) des im ersten Bezugssystem nachweisbaren Gravitationsfeldes und einem Trägheitsfeld. Wird das zweite Bezugsystem linear gegen das erste beschleunigt, ist das Trägheitsfeld homogen und seine Stärke gleich minus die Relativbeschleunigung.