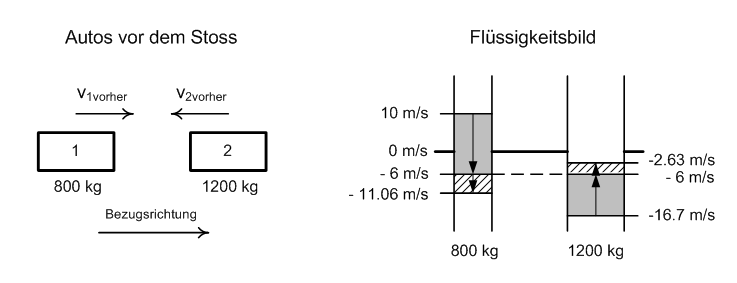
Lösung zu Frontalkollision
- Der Impuls verteilt sich beim Stoss auf beide Fahrzeuge [math]v_{in} = \frac {800 kg \cdot 10 m/s + 1200 kg \cdot (-16.67 m/s)}{800 kg + 1200 kg}[/math] = -6 m/s. Die Fahrzeuge bewegen sich gemeinsam gegen die Bezugsrichtung.
- Der durch die Knautschzone fliessende Impuls (schattierte Fläche in Skizze, 800kg*(10m/s - (-6m/s)) = 12.8 kNs) durchfällt eine mittlere Geschwindigkeitsdifferenz von 13.33 m/s (Differenz zwischen den Geschwindigkeitsmittelwerten (10 m/s + -6 m/s)/2 = 2 m/s und (-16.67 m/s + -6 m/s)/2 = -11.33 m/s) und setzt dabei 13.33 m/s * 12.8 kNs = 170.6 kJ Energie frei.
- Die umgesetzte Energie nimmt quadratisch mit der Geschwindigkeitsänderung (vrel) bezüglich der Geschwindigkeit des Massenmittelpunktes (vin) zu. Falls nun 10% der freigesetzten Energie von den Knautschzonen an den Impulsstrom zurückgegeben wird, überschwingen die Relativgeschwindigkeiten (Pegel im Flüssigkeitsbild) um 31.6% (die Wurzel aus 0.1 ist 0.316). Demnach beträgt die Geschwindigkeit des leichteren Fahrzeuges nach diesem teilelastischen Stoss etwa -11.06 m/s. Die Geschwindigkeit des schwereren Fahrzeuges erhöht sich auf -2.63 m/s.
Die letzte Frage lässt sich auch formal lösen. Die Knautschzone gibt 17.07 kJ Energie zurück. Damit kann eine bestimmte Impulsmenge Δp im Mittel um Δv gehoben werden. Mit der zur Verfügung stehenden Energie lässt sich die folgende "Impulspumparbeit" verrichten
- [math]W = \Delta p \Delta v_{mittel} = m_1 v_{r1}\frac {v_{r1} + v_{r2}}{2} = \frac {m_1(v_{r1})2}{2}(1 + \frac {m_1}{m_2})[/math]
oder
- [math]v_{r1} = \sqrt{\frac {2 W}{m_1(1 + \frac {m_1}{m_2})}}[/math] = 5.06 m/s
Die Geschwindigkeit des leichteren Fahrzeuges nimmt um 5.06 m/s von -6 m/s auf -11.06 m/s ab. Die Geschwindigkeit des schwereren Fahrzeuges nimmt um 3.37 m/s von -6 m/s auf -2.63 m/s zu.