Lösung zu Luftspeicher
-
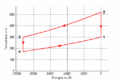
T-S-Diagramm
-
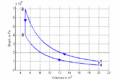
p-V-Diagramm
- Im T-S-Diagramm bilden die Isentropen vertikale Linien, die Isochoren verlaufen exponentiell in Funktion der Entropie oder logarithmisch mit der Temperatur. Im p-V-Diagramm schneiden die Isentropen die Isothermen unter einem spitzen Winkel, die Isochoren verlaufen vertikal.
- Am Ende des ersten Teilprozesses beträgt der Druck [math]p_2=p_1\left(\frac {V_1}{V_2}\right)^\kappa[/math] = 1 bar * (20 l / 5 l)1.4 = 6.96 bar und die Temperatur ist gleich [math]T_2=T_1\frac{p_2V_2}{p_1V_1}[/math] = 300 K * (6.96 bar * 5 l)/(1 bar * 20 l) = 522 K. Nach dem zweiten Teilprozess betragen das Volumen V3 = 5 l, die Temperatur T3 = 300 K und der Druck p3 = p1 * V1 / V3 = 1 bar * 20 l / 5 l = 4 bar. Nach dem dritten Teilprozess beträgt der Druck nur noch [math]p_4 = p_3\left(\frac {V_3}{V_4}\right)^\kappa[/math] = 4 bar * (5 l / 20 l)1.4 = 0.574 bar und die Temperatur misst [math]T_4 = T_3 \frac{p_4 V_4}{p_3 V_3}[/math] = 300 K * (0.574 bar * 20 l)/(4 bar * 5 l) = 172 K. Für die Berechnung dieser Werte geht man am besten vom Anfangszustand des isentropen Teilprozesses aus und verwendet dann die Isentropengleichung und die thermische Zustandsgleichung.
- Die Arbeit bei den isentropen Prozessen ist gleich der Änderung der inneren Energie. Diese hängt wiederum nur von der Temperatur ab [math]W_{tot}=W_{12}+W_{23}=n\hat c_V(T_2-T_1+T_4-T_3)=n\hat c_V(T_2+T_4-2T_1)[/math] = 1.57 MJ.
- Im zweiten Teilprozess, der isochoren Auskühlung, beträgt die Änderung der inneren Energie [math]\Delta W=n\hat c_V(T_3-T_2)[/math] = -3.7 MJ. Die zugehörige Entropieänderung ist gleich [math]\Delta S=n\hat c_V\ln\left(\frac{T_3}{T_2}\right)[/math] = -9.2 kJ/K.